题目内容
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(
(α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(![]() )=2
)=2![]() .
.
(Ⅰ)求曲线C和直线l在该直角坐标系下的普通方程;
(Ⅱ)动点A在曲线C上,动点B在直线l上,定点P的坐标为(﹣2,2),求|PB|+|AB|的最小值.
【答案】解:(Ⅰ)∵曲线C的参数方程为![]() (α为参数),
(α为参数),
∴曲线C的直角坐标方程为(x﹣1)2+y2=1.
∵直线l的极坐标方程为ρsin(![]() )=2
)=2![]()
∴![]() =2
=2![]() ,
,
ρsinθ+ρcosθ=4,
∴直线l直角坐标方程为x+y﹣4=0.
(Ⅱ)如图,P关于y=﹣x+4对称点P'(x,y),
|P'C|﹣r=P'A=P'A=|P'B|=P'B|+|A'B|,
此时P'BA共成共线,|PB|+|AB|取最小值,
又![]() ,解得x=2,y=6,
,解得x=2,y=6,
∴|PA'|=![]() ﹣1=
﹣1=![]() ,
,
∴![]() -1.
-1.
∴|PB|+|AB|的最小值是![]() -1..
-1..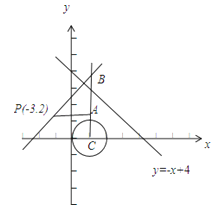
【解析】(Ⅰ)由曲线C的参数方程能求出曲线C的直角坐标方程,由直线l的极坐标方程能求出直线l直角坐标方程.
(Ⅱ)及民,象,P(﹣2,2),利用两点意距离公式能求出|PB|+|AB|取最小值.

练习册系列答案
相关题目