Question

【题目】如图，在三棱锥P﹣ABC中，△ABC是边长为2的正三角形，∠PCA=90°，E，H分别为AP，AC的中点，AP=4，BE= ．
（Ⅰ）求证：AC⊥平面BEH；
（Ⅱ）求直线PA与平面ABC所成角的正弦值．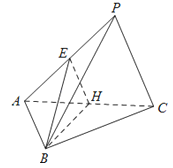

Answer 1

【答案】证明：（Ⅰ）因为△ABC是边长为2的正三角形，
所以BH⊥AC．
又因为E，H分别为AP，AC的中点，得EH∥PC，
因为∠PCA=90°，
所以EH⊥AC．
故AC⊥平面BEH．
（Ⅱ）解：取BH得中点G，连接AG．
因为EH=BH=BE=，所以EG⊥BH．
又因为AC⊥平面BEH，所以EG⊥AC，
所以EG⊥平面ABC．
所以∠EAG为PA与平面ABC所成的角．
在直角三角形EAG中，AE=2，EG=，
所以\sin∠EAG==．
所以PA与平面ABC所成的角的正弦值为．

【解析】（Ⅰ）证明：BH⊥AC，EH⊥AC，即可证明AC⊥平面BEH；
（Ⅱ）取BH得中点G，连接AG，证明∠EAG为PA与平面ABC所成的角，即可求直线PA与平面ABC所成角的正弦值．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则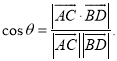才能正确解答此题．