题目内容
【题目】一个多面体的直观图，正（主）视图，侧（左）视图如下所示，其中正（主）视图、侧（左）视图为边长为a的正方形．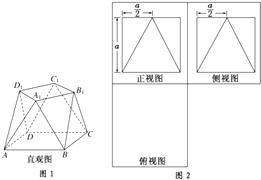 
（1）请在指定的框内画出多面体的俯视图；
（2）若多面体底面对角线AC，BD交于点O，E为线段AA1的中点，求证：OE∥平面A1C1C；
（3）求该多面体的表面积．
【答案】
（1）解：根据多面体的直观图、正（主）视图、侧（左）视图，得到俯视图如下：
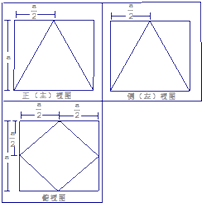
（2）证明：如图，连接AC，BD交于O点，
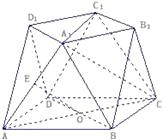
因为E为AA1的中点，O为AC的中点，所以在△AA1C中，OE为△AA1C的中位线，
所以OE∥A1C，∵OE平面A1C1C，A1C1平面A1C1C，
所以OE∥平面A1C1C
（3）解：由三示图可知多面体表面共包括10个面，SABCD=a2， 
， 
， 
，
所以表面积 
．
【解析】（1）根据多面体的直观图、正（主）视图、侧（左）视图，得到俯视图．（2）连接AC，BD交于O点，因为E为AA1的中点，可得OE为△AA1C的中位线，OE∥A1C，从而证得OE∥平面A1C1C．（3）由三示图可知多面体表面共包括10个面，SABCD=a2 ， ，再求出 
， 
的值，由表面积 
，运算求出结果．
【考点精析】利用简单空间图形的三视图和直线与平面平行的判定对题目进行判断即可得到答案，需要熟知画三视图的原则：长对齐、高对齐、宽相等；平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
练习册系列答案
相关题目
