题目内容
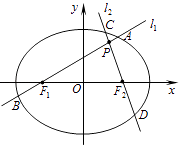
【题目】分别过椭圆E: ![]() =1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2
=1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2 ![]() ,|CD|=
,|CD|= ![]() .
. 
(1)求椭圆E的方程;
(2)是否存在定点M,N,使得|PM|+|PN|为定值?若存在,求出M、N点坐标,若不存在,说明理由.
【答案】
(1)解:当l1与x轴重合时,k1+k2=k3+k4=0,
即k3=﹣k4,
∴l2垂直于x轴,得|AB|=2a=2 ![]() ,|CD|=
,|CD|= ![]() ,
,
解得a= ![]() ,b=
,b= ![]() ,
,
∴椭圆E的方程为 ![]()
(2)解:焦点F1、F2坐标分别为(﹣1,0),(1,0),
当直线l1或l2斜率不存在时,P点坐标为(﹣1,0)或(1,0),
当直线l1,l2斜率存在时,设斜率分别为m1,m2,
设A(x1,y1),B(x2,y2),由 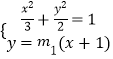 ,
,
得 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
同理k3+k4= ![]() ,
,
∵k1+k2=k3+k4,
∴ ![]() ,即(m1m2+2)(m2﹣m1)=0,
,即(m1m2+2)(m2﹣m1)=0,
由题意知m1≠m2,
∴m1m2+2=0,
设P(x,y),则 ![]() ,
,
即 ![]() ,x≠±1,
,x≠±1,
由当直线l1或l2斜率不存在时,
P点坐标为(﹣1,0)或(1,0)也满足,
∴点P(x,y)点在椭圆 ![]() 上,
上,
∴存在点M,N其坐标分别为(0,﹣1)、(0,1),
使得|PM|+|PN|为定值2 ![]()
【解析】(1)由已知条件推导出|AB|=2a=2 ![]() ,|CD|=
,|CD|= ![]() ,由此能求出椭圆E的方程.(2)焦点F1、F2坐标分别为(﹣1,0),(1,0),当直线l1或l2斜率不存在时,P点坐标为(﹣1,0)或(1,0),当直线l1 , l2斜率存在时,设斜率分别为m1 , m2 , 设A(x1 , y1),B(x2 , y2),由
,由此能求出椭圆E的方程.(2)焦点F1、F2坐标分别为(﹣1,0),(1,0),当直线l1或l2斜率不存在时,P点坐标为(﹣1,0)或(1,0),当直线l1 , l2斜率存在时,设斜率分别为m1 , m2 , 设A(x1 , y1),B(x2 , y2),由 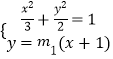 ,得
,得 ![]() ,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,﹣1)、(0,1),使得|PM|+|PN|为定值2
,由此利用韦达定理结合题设条件能推导出存在点M,N其坐标分别为(0,﹣1)、(0,1),使得|PM|+|PN|为定值2 ![]() .
.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案