题目内容
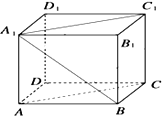
【题目】如图，长方体ABCD﹣A1B1C1D1中，AA1=AB=2，AD=1，E，F，G分别是DD1 ， AB，CC1的中点，则异面直线A1E与GF所成角为（ ）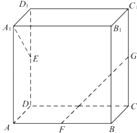 
A.30°
B.45°
C.60°
D.90°
【答案】D
【解析】解：如图：连接B1G，EG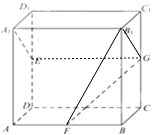 
∵E，G分别是DD1 ， CC1的中点，
∴A1B1∥EG，A1B1=EG，∴四边形A1B1GE为平行四边形
∴A1E∥B1G，∴∠B1GF即为异面直线A1E与GF所成的角
在三角形B1GF中，B1G= 
= 
= 
FG= 
= 
= 
B1F= 
= 
= 
∵B1G2+FG2=B1F2
∴∠B1GF=90°
∴异面直线A1E与GF所成角为90°
故选 D
连接B1G，EG，先利用长方形的特点，证明四边形A1B1GE为平行四边形，从而A1E∥B1G，所以∠B1GF即为异面直线A1E与GF所成的角，再在三角形B1GF中，分别计算三边的长度，利用勾股定理即可得此角的大小
练习册系列答案
相关题目
