Question

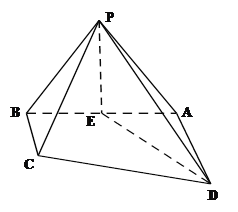
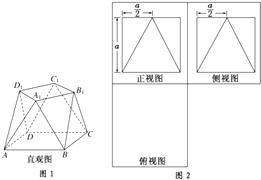
【题目】如图，边长为2的正方形ABCD中，
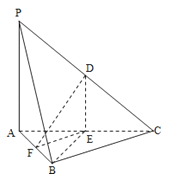
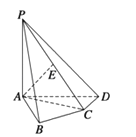
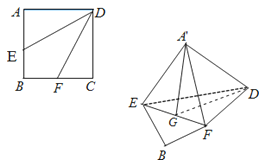
（1）点E是AB的中点，点F是BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．求证：A′D⊥EF．
（2）当BE=BF=BC时，求三棱锥A′﹣EFD体积．

Answer 1

【答案】（1）证明：由已知，折叠前，有AD⊥AE，CD⊥CF，
折叠后，有A′D⊥A′E，A′D⊥A′F，
又∵A′E∩A′F=A′，A′E、A′F平面A′EF，
∴A′D⊥平面A′EF，
∵EF平面A′EF，
∴A′D⊥EF；
（2）解：取EF的中点G，连接A′G，则
由BE=BF=BC可知，
△A′EF为腰长，底边长为的等腰三角形，
∴=，则=XX=
与（1）同理可得，A′D⊥平面A′EF，且A′D=2，
∴=XX2=．

【解析】（1）利用折叠前后直角不变，结合线面垂直的判定得到A′D⊥平面A′EF，从而得到A′D⊥EF；
（2）求出△A′EF的面积，结合DA′⊥面A′EF，利用等积法把三棱锥A′﹣EFD体积转化为三棱锥D﹣A′EF的体积求解．