题目内容
已知平面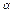 ∥
∥ ,在
,在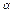 内有4个点,在
内有4个点,在 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
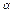 ∥
∥ ,在
,在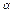 内有4个点,在
内有4个点,在 内有6个点.
内有6个点.(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
(1)98 (2)194 (3)114
(1)所作出的平面有三类:①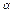 内1点,
内1点, 内2点确定的平面,有C
内2点确定的平面,有C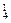 ·C
·C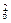 个;②
个;②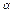 内2点,
内2点, 内1点确定的平面,有C
内1点确定的平面,有C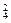 ·C
·C 个;③
个;③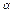 ,
, 本身.
本身.
∴所作的平面最多有C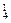 ·C
·C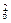 +C
+C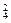 ·C
·C +2=98(个).
+2=98(个).
(2)所作的三棱锥有三类:①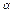 内1点,
内1点, 内3点确定的三棱锥,有C
内3点确定的三棱锥,有C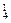 ·C
·C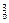 个;②
个;②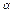 内2点,
内2点, 内2点确定的三棱锥,有C
内2点确定的三棱锥,有C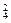 ·C
·C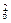 个;
个;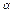 内3点,
内3点, 内1点确定的三棱锥,有C
内1点确定的三棱锥,有C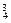 ·C
·C 个.
个.
∴最多可作出的三棱锥有:C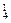 ·C
·C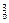 +C
+C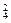 ·C
·C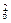 +C
+C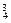 ·C
·C =194(个).
=194(个).
(3)∵当等底面积、等高的情况下三棱锥的体积相等,
且平面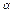 ∥
∥ ,∴体积不相同的三棱锥最多有
,∴体积不相同的三棱锥最多有
C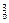 +C
+C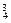 +C
+C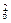 ·C
·C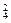 =114(个).
=114(个).
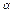 内1点,
内1点, 内2点确定的平面,有C
内2点确定的平面,有C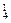 ·C
·C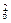 个;②
个;②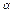 内2点,
内2点, 内1点确定的平面,有C
内1点确定的平面,有C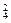 ·C
·C 个;③
个;③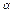 ,
, 本身.
本身.∴所作的平面最多有C
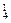 ·C
·C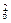 +C
+C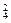 ·C
·C +2=98(个).
+2=98(个).(2)所作的三棱锥有三类:①
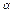 内1点,
内1点, 内3点确定的三棱锥,有C
内3点确定的三棱锥,有C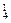 ·C
·C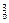 个;②
个;②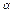 内2点,
内2点, 内2点确定的三棱锥,有C
内2点确定的三棱锥,有C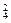 ·C
·C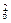 个;
个;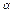 内3点,
内3点, 内1点确定的三棱锥,有C
内1点确定的三棱锥,有C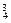 ·C
·C 个.
个.∴最多可作出的三棱锥有:C
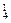 ·C
·C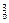 +C
+C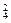 ·C
·C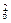 +C
+C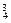 ·C
·C =194(个).
=194(个).(3)∵当等底面积、等高的情况下三棱锥的体积相等,
且平面
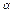 ∥
∥ ,∴体积不相同的三棱锥最多有
,∴体积不相同的三棱锥最多有C
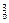 +C
+C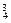 +C
+C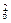 ·C
·C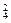 =114(个).
=114(个).
练习册系列答案
相关题目
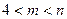 ,
,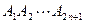 是一个正2n+1边形,
是一个正2n+1边形,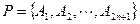 .求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
.求顶点属于P且恰有两个内角是锐角的凸m边形的个数. +
+ ; ②
; ②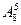
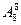 .
.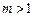 ),则客运车票增加了62种,问原有多少个车站?现有多少个车站?
),则客运车票增加了62种,问原有多少个车站?现有多少个车站?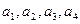 是
是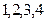 的任一排列,
的任一排列,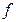 是
是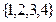 到
到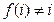 ,记数表
,记数表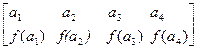 。若数表
。若数表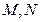 的对应位置上至少有一个不同,就说
的对应位置上至少有一个不同,就说 =___________________.
=___________________.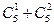 的值为______.
的值为______.