题目内容
设m,n是给定的整数,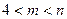 ,
,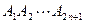 是一个正2n+1边形,
是一个正2n+1边形,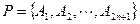 .求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
.求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
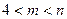 ,
,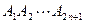 是一个正2n+1边形,
是一个正2n+1边形,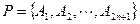 .求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
.求顶点属于P且恰有两个内角是锐角的凸m边形的个数.见解析
先证一个引理:顶点在P中的凸m边形至多有两个锐角,且有两个锐角时,这两个锐角必相邻.
事实上,设这个凸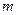 边形为
边形为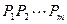 ,只考虑至少有一个锐角的情况,此时不妨设
,只考虑至少有一个锐角的情况,此时不妨设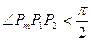 ,
,
则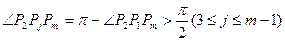 ,
, 

更有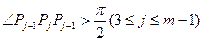 .
.
而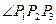 +
+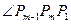
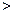
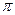 ,故其中至多一个为锐角,这就证明了引理.
,故其中至多一个为锐角,这就证明了引理.
由引理知,若凸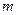 边形中恰有两个内角是锐角,则它们对应的顶点相邻.
边形中恰有两个内角是锐角,则它们对应的顶点相邻.
在凸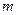 边形中,设顶点
边形中,设顶点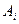 与
与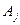 为两个相邻顶点,且在这两个顶点处的内角均为锐角.设
为两个相邻顶点,且在这两个顶点处的内角均为锐角.设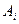 与
与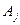 的劣弧上包含了
的劣弧上包含了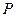 的
的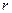 条边(
条边(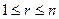 ),这样的
),这样的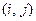 在
在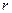 固定时恰有
固定时恰有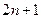 对.
对.
(1)若凸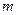 边形的其余
边形的其余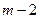 个顶点全在劣弧
个顶点全在劣弧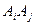 上,而
上,而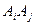 劣弧上有
劣弧上有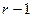 个
个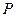 中的点,此时这
中的点,此时这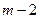 个顶点的取法数为
个顶点的取法数为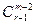 .
.
(2)若凸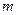 边形的其余
边形的其余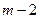 个顶点全在优弧
个顶点全在优弧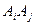 上,取
上,取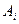 ,
,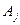 的对径点
的对径点 ,
, ,由于凸
,由于凸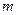 边形在顶点
边形在顶点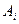 ,
,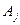 处的内角为锐角,所以,其余的
处的内角为锐角,所以,其余的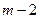 个顶点全在劣弧
个顶点全在劣弧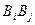 上,而劣弧
上,而劣弧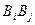 上恰有
上恰有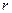 个
个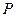 中的点,此时这
中的点,此时这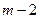 个顶点的取法数为
个顶点的取法数为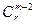 .
.
所以,满足题设的凸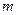 边形的个数为
边形的个数为
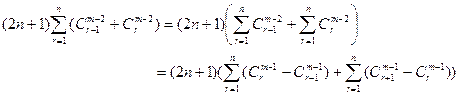
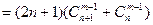 .
.
事实上,设这个凸
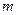 边形为
边形为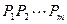 ,只考虑至少有一个锐角的情况,此时不妨设
,只考虑至少有一个锐角的情况,此时不妨设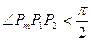 ,
,则
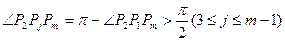 ,
, 

更有
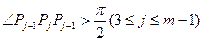 .
.而
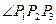 +
+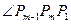
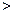
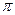 ,故其中至多一个为锐角,这就证明了引理.
,故其中至多一个为锐角,这就证明了引理.由引理知,若凸
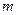 边形中恰有两个内角是锐角,则它们对应的顶点相邻.
边形中恰有两个内角是锐角,则它们对应的顶点相邻.在凸
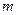 边形中,设顶点
边形中,设顶点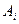 与
与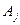 为两个相邻顶点,且在这两个顶点处的内角均为锐角.设
为两个相邻顶点,且在这两个顶点处的内角均为锐角.设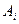 与
与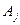 的劣弧上包含了
的劣弧上包含了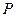 的
的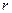 条边(
条边(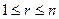 ),这样的
),这样的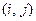 在
在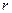 固定时恰有
固定时恰有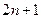 对.
对.(1)若凸
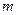 边形的其余
边形的其余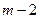 个顶点全在劣弧
个顶点全在劣弧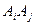 上,而
上,而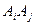 劣弧上有
劣弧上有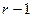 个
个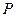 中的点,此时这
中的点,此时这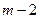 个顶点的取法数为
个顶点的取法数为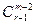 .
.(2)若凸
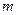 边形的其余
边形的其余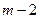 个顶点全在优弧
个顶点全在优弧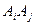 上,取
上,取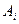 ,
,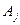 的对径点
的对径点 ,
, ,由于凸
,由于凸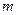 边形在顶点
边形在顶点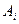 ,
,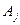 处的内角为锐角,所以,其余的
处的内角为锐角,所以,其余的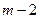 个顶点全在劣弧
个顶点全在劣弧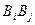 上,而劣弧
上,而劣弧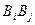 上恰有
上恰有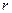 个
个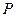 中的点,此时这
中的点,此时这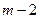 个顶点的取法数为
个顶点的取法数为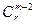 .
.所以,满足题设的凸
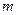 边形的个数为
边形的个数为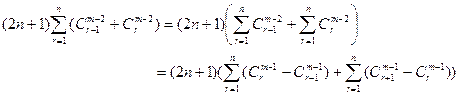
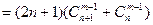 .
.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
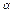 ∥
∥ ,在
,在