题目内容
8.已知f(x)是二次函数且f(0)=2,f(2-x)-f(x)=0,f(1)=-2,则f(x)=4x2-8x+2.(提示:已知函数模型.可用待定系数法)分析 设出函数的解析式,利用条件确定参数,即可得出结论.
解答 解:f(0)=2,则可设f(x)=ax2+bx+2.
∵f(2-x)=f(x),∴f(1+1-x)=f[1-(1-x)]
∴x=1为函数的对称轴,
∴x=-$\frac{b}{2a}$=1,∴b=-2a
∵f(1)=-2,∴a+b+2=-2,
∴a-2a+2=-2,
∴a=4,
∴b=-8,
∴f(x)=4x2-8x+2.
故答案为:4x2-8x+2.
点评 本题考查函数的解析式,考查待定系数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
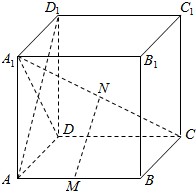 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证:
如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC,求证: