题目内容

6．有4名学生和3位老师排成一排照相，规定两端不排老师且老师顺序固定不变，那么不同的排法有240．

分析 先计算出2名学生排在两端，剩下的学生和老师全排的种数，再除以3位老师的顺序数，问题得以解决．

解答 解：先选2名学生排在两端，剩下的学生和老师全排有${A}_{4}^{2}•{A}_{5}^{5}$，因为老师的顺序有${A}_{3}^{3}$=6种，
故规定两端不排老师且老师顺序固定不变，那么不同的排法有$\frac{{A}_{4}^{2}•{A}_{5}^{5}}{{A}_{3}^{3}}$=240种，
故答案为：240

点评 本题主要考查了排列问题中的站队问题，特殊元素优先安排的原则是关键，属于中档题．

练习册系列答案
相关题目
16．一台晚会有6个节目，其中有2个小品，如果2个小品不连续演出，共有不同的演出顺序多少种？
17．在极坐标系中，已知曲线C：ρ2+2ρsinθ+$\frac{3}{4}$=0（ρ∈R），l为过定点（2，-1）且与直线θ=$\frac{π}{4}$平行的直线，A、B分别为曲线C和直线l上的动点．
（1）将曲线C和直线l分别化为直角坐标系下的方程；
（2）求|AB|的最小值．
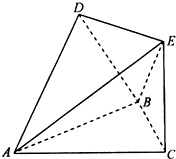14．如图，△ABC是边长为4的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=2．
（1）证明：DE∥平面ABC；
（2）证明：AD⊥BE．
1．已知函数f（x）=$\frac{{x}^{2}-ax}{lnx}$
（1）若f（x）＞0对其定义域内任意x成立，求a的值；
（2）当a=0时，求f（x）在区间[e${\;}^{\frac{1}{4}}$，e]上最值．
11．在△ABC中，内角A，B，C的对边分别为a，b，c，若a=1，b=3，C=120°，则边c的长度为$\sqrt{13}$．
18．已知函数f（x）=ax2-（2a+1）x+lnx，a∈R．
（1）当a=1时，求f（x）的单调区间和极值；
（2）若关于x的方程f（x）=2ax2-2（a+1）x恰有两个不等的实根，求实数a的取值范围；
（3）设g（x）=ex-x-1，若对任意的x1∈（0，+∞），x2∈R，不等式f（x1）≤g（x2）恒成立，求实数a的取值范围．
15．解不等式组$\left\{\begin{array}{l}{{x}^{2}+2|x|-3＜0}\\{|{x}^{2}-x|≤2}\end{array}\right.$．
16．如图，三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，AC=BC，D、E、F分别为棱AB，BC，A1C1的中点．
（1）证明：EF∥平面A1CD；
（2）证明：平面A1CD⊥平面ABB1A1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网