题目内容
16. 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,AC=BC,D、E、F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,AC=BC,D、E、F分别为棱AB,BC,A1C1的中点.(1)证明:EF∥平面A1CD;
(2)证明:平面A1CD⊥平面ABB1A1.
分析 (1)根据线面平行的判定定理证明EF∥A1D即可证明EF∥平面A1CD;
(2)根据面面垂直的判定定理即可证明平面A1CD⊥平面ABB1A1.
解答 证明:(1)连结DE,
∵D,E分别是AB,BC的中点
∴DE∥AC,DE=$\frac{1}{2}$AC,
∵F为棱A1C1的中点.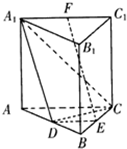
∴A1F=$\frac{1}{2}$A1C1,
∴A1F∥$\frac{1}{2}$AC,
即DE∥A1F,DE=A1F,
∴四边形A1DEF为平行四边形,
∴A1D∥EF
又∵EF?平面A1CD,A1D?平面A1CD,
∴EF∥平面A1CD.
(2)∵A1A⊥平面ABC,CD?平面ABC,
∴AA1⊥CD,
∵AC=BC,D为AB的中点,
∴AB⊥CD,
∵A1A∩AB=A
∴CD⊥平面ABB1A1
∵CD?平面A1CD,
∴平面A1CD⊥平面ABB1A1.
点评 本题主要考查空间直线和平面平行以及平面和平面垂直的判定,要求熟练掌握相应的判定定理.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1,
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=1, 如图是一个长方体ABCD-A1B1C1D1被一个平面截去一部分后,所得多面体的直观图,已知AB=6,AD=AA1=4,BE=CF=2.
如图是一个长方体ABCD-A1B1C1D1被一个平面截去一部分后,所得多面体的直观图,已知AB=6,AD=AA1=4,BE=CF=2. 如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,且PD=PC=BC=3,CD=3$\sqrt{2}$,E为PB中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,且PD=PC=BC=3,CD=3$\sqrt{2}$,E为PB中点. 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.