题目内容
14.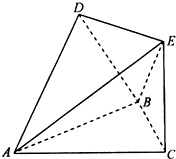 如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.(1)证明:DE∥平面ABC;
(2)证明:AD⊥BE.
分析 (1)取AB的中点F,连接DF,CF,由已知可证DF$\stackrel{∥}{=}$EC,可得四边形DEFC为平行四边形,可得DE∥FC,由DE?平面ABC,从而可证DE∥平面ABC.
(2)以FA,FC,FD为x,y,z轴的正方向建立直角坐标系,求出向量$\overrightarrow{AD}$,$\overrightarrow{BE}$的坐标,由$\overrightarrow{AD}$•$\overrightarrow{BE}$=0,即可证明AD⊥BE.
解答  证明:(1)取AB的中点F,连接DF,CF,
证明:(1)取AB的中点F,连接DF,CF,
∵△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,
∴DF⊥CF,
∵DF=$\frac{1}{2}$BC=2
又∵EC⊥平面ABC,既有:EC⊥FC,EC=2.
∴DF$\stackrel{∥}{=}$EC,故四边形DEFC为平行四边形,
∴DE∥FC
∴DE?平面ABC,可得DE∥平面ABC.
(2)以FA,FC,FD为x,y,z轴的正方向建立直角坐标系,
则有:A(2,0,0),D(0,0,2),B(-2,0,0),E(0,2$\sqrt{3}$,2)
$\overrightarrow{AD}$=(-2,0,2),$\overrightarrow{BE}$=(-2,2$\sqrt{3}$,2)
由于$\overrightarrow{AD}$•$\overrightarrow{BE}$=0,
故AD⊥BE.
点评 本题主要考查了直线与平面平行的判定,空间中直线与直线之间的位置关系,考查了空间想象能力和转化思想,属于基本知识的考查.

练习册系列答案
相关题目
4.某学校对学生进行三项身体素质测试,每项测试的成绩有3分、2分、1分,若各项成绩均不小于2分切三项测试分数之和不小于7分的学生,则其身体素质等级记为优秀;若三项测试分数之和小于6分,则该学生身体素质等级记为不合格,随机抽取10名学生的成绩记录如下表:
(1)利用上表提供的数据估算该学校学生身体素质的优秀率;
(2)从表中身体素质等级记为不合格的学生中任意抽取2人组成小组加强锻炼,求这2人三项测试总分相同的概率.
| 学生编号 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 |
| 三项成绩 | 2,1,2 | 1,2,2 | 2,3,2 | 3,1,1 | 3,2,2 | 2,3,1 | 3,3,3 | 1,1,1 | 3,3,1 | 2,2,2 |
(2)从表中身体素质等级记为不合格的学生中任意抽取2人组成小组加强锻炼,求这2人三项测试总分相同的概率.
5.已知P为抛物线C:y2=8x准线上任意一点,A(1,3)、B(1,-3),则△PAB的面积为( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
 要在一个半径为R的半圆形铁板中截取一块面积最大的矩形ABCD,问应如何截取,并求此矩形的面积.
要在一个半径为R的半圆形铁板中截取一块面积最大的矩形ABCD,问应如何截取,并求此矩形的面积.