题目内容
8.已知数列{an}满足an≠0,a1=$\frac{1}{3}$,an-1-an=2an•an-1(n≥2,n∈N*).(1)求证:$({\frac{1}{a_n}})$是等差数列;
(2)设bn=an•an+1,{bn}的前n项和为Sn,求证:Sn<$\frac{1}{6}$.
分析 (1)由题意化简已知的式子,由条件求出数列{$\frac{1}{{a}_{n}}$}的首项,根据等差数列的定义即可证明结论;
(2)由(1)和等差数列的通项公式求出$\frac{1}{{a}_{n}}$,化简后代入bn化简,利用裂项相消法求出数列{bn}的前n项和Sn,即可证明结论.
解答 证明:(1)∵an-1-an=2an•an-1(n≥2),an≠0,
∴两边同除anan-1,得$\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}=2$(n≥2),
又a1=$\frac{1}{3}$,
∴$\left\{{\frac{1}{a_n}}\right\}$是以3为首项,2为公差的等差数列.…(6分)
(2)由(1)知:$\frac{1}{a_n}=3+({n-1})•2=2n+1$,
∴${a_n}=\frac{1}{2n+1}$…(8分)
∴${b_n}={a_n}•{a_{n+1}}=\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$($\frac{1}{2n+1}-\frac{1}{2n+3}$),
则${S}_{n}=\frac{1}{2}[(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})+…+(\frac{1}{2n+1}-\frac{1}{2n+3})]$
=$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+3})=\frac{1}{6}-\frac{1}{4n+6}$,
∴${S_n}<\frac{1}{6}$…(12分).
点评 本题考查了等差数列的定义、通项公式,以及裂项相消法求数列的前n项和,是数列与不等式的综合题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.将单位正方体放置在水平桌面上(一面与桌面完全接触),沿其一条棱翻动一次后,使得正方体的另一面与桌面完全接触,称一次翻转.如图,正方体的顶点 A,经任意翻转三次后,点 A与其终结位置的直线距离不可能为( )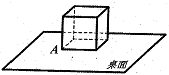

| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
18.掷骰子2次,每个结果以(x,y)记之,其中x1,x2分别表示第一颗,第二颗骰子的点数,设A{(x1,x2)|x1+x2=8},B={(x1,x2)|x1>x2},则P(B|A)( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
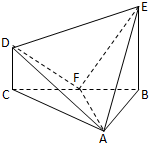 在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.