题目内容
定义在R上的奇函数 ,当
,当 ,
,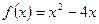
(1)作出函数 的图象
的图象
(2)求函数 的表达式
的表达式
(3)求满足方程 的解
的解
(1)略
(2)
(3)
解析

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
题目内容
定义在R上的奇函数 ,当
,当 ,
,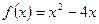
(1)作出函数 的图象
的图象
(2)求函数 的表达式
的表达式
(3)求满足方程 的解
的解
(1)略
(2)
(3)
解析

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案