题目内容
17.已知f(x)=x5-ax3+bx-6,f(-2)=10,则f(2)=-22.分析 由f(-2)=10,a,b的值不确定,可以得出a,b的关系式,整体代入f(2)的表达式中,计算求解.
解答 解:f(x)=x5-ax3+bx-6,且f(-2)=10,即-32-8a-2b-6=10,整理得,8a+2b=-48,
∴f(2)=32+8a+2b-6=-22.
故答案为:-22.
点评 本题考查函数值的计算,考查整体代换,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
2.若a≠b,则关于x的不等式$\frac{{x-{a^2}-{b^2}}}{x-2ab}≥0$的解集是( )
| A. | {x|x<2ab或x≥a2+b2} | B. | {x|x≤2ab或x≥a2+b2} | C. | {x|x<2ab或x>a2+b2} | D. | {x|2ab<x≤a2+b2} |
9.若直线ax-by+2=0(a>0,b>0)经过圆x2+y2+4x-4y-1=0的圆心,则$\frac{2}{a}+\frac{3}{b}$的最小值为( )
| A. | 10 | B. | $4+2\sqrt{6}$ | C. | $5+2\sqrt{6}$ | D. | $4\sqrt{6}$ |
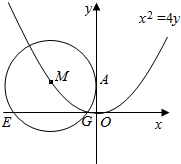 设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?
设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么? 如图所示.已知E、F、G、H分别是四边形ABCD各边的中点.若EG⊥FH,求证:AC=BD.
如图所示.已知E、F、G、H分别是四边形ABCD各边的中点.若EG⊥FH,求证:AC=BD.