题目内容
5.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a2-b2=c2,c>0)与y轴正半轴的交点为B,点P在椭圆上,则|BP|的最大值为( )| A. | 2b | B. | $\frac{{a}^{2}}{c}$ | C. | 2b或$\frac{{b}^{2}}{c}$ | D. | 2b或$\frac{{a}^{2}}{c}$ |
分析 根据椭圆的方程得到B(0,b),P点在椭圆上,从而可设P(acosθ,bsinθ),根据两点间距离公式并配方可以得到$|BP|=\sqrt{-{c}^{2}(sinθ+\frac{{b}^{2}}{{c}^{2}})^{2}+{a}^{2}+{b}^{2}+\frac{{b}^{4}}{{c}^{2}}}$,可以看出要求|BP|的最大值,需讨论b,c关系:b>c时,sinθ=-1时,|BP|取到最大值;b≤c时,sinθ=$-\frac{{b}^{2}}{{c}^{2}}$时,|BP|取到最大值,这样求出这两种情况下的最大值即可找出正确选项.
解答 解:根据条件知,B(0,b),设P(acosθ,bsinθ),则:
$|BP|=\sqrt{{a}^{2}co{s}^{2}θ+{b}^{2}(sinθ-1)^{2}}$
=$\sqrt{{a}^{2}co{s}^{2}θ+{b}^{2}si{n}^{2}θ-2{b}^{2}sinθ+{b}^{2}}$
=$\sqrt{-{c}^{2}si{n}^{2}θ-2{b}^{2}sinθ+{a}^{2}+{b}^{2}}$
=$\sqrt{-{c}^{2}(sinθ+\frac{{b}^{2}}{{c}^{2}})^{2}+{a}^{2}+{b}^{2}+\frac{{b}^{4}}{{c}^{2}}}$
∴①若b>c,则$\frac{{b}^{2}}{{c}^{2}}>1$;
∴sinθ=-1时,|BP|取最大值$\sqrt{-{c}^{2}(-1+\frac{{b}^{2}}{{c}^{2}})^{2}+{a}^{2}+{b}^{2}+\frac{{b}^{4}}{{c}^{2}}}$=$\sqrt{2{b}^{2}+2{b}^{2}}=2b$;
②若b≤c,则$0<\frac{{b}^{2}}{{c}^{2}}≤1$;
∴sin$θ=-\frac{{b}^{2}}{{c}^{2}}$时,|BP|取最大值$\sqrt{{a}^{2}+{b}^{2}+\frac{{b}^{4}}{{c}^{2}}}=\sqrt{\frac{{a}^{2}{c}^{2}+{b}^{2}{c}^{2}+{b}^{4}}{{c}^{2}}}$=$\frac{{a}^{2}}{c}$;
∴|BP|的最大值为2b或$\frac{{a}^{2}}{c}$.
故选:D.
点评 考查椭圆的标准方程,椭圆上点设成(acosθ,bsinθ)是本题求解的关键,这样可将两个变量x,y变成一个变量θ,便于求最值,以及两点间距离公式,配方求二次式子的最值的方法.

| A. | x=2是f(x)的极小值点 | |
| B. | 函数y=f(x)-x有且只有1个零点 | |
| C. | 存在正实数k,使得f(x)>kx恒成立 | |
| D. | 对任意两个正实数x1,x2,且x2>x1,若f(x1)=f(x2),则x1+x2>4 |
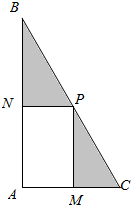 某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].