题目内容
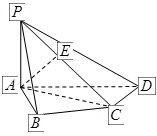
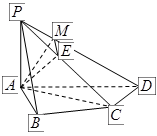
(12分)如图,在四棱锥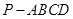 中,
中,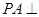 底面
底面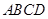 ,
,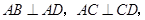
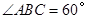 ,
,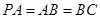 ,
,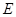 是
是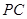 的中点.
的中点.
(Ⅰ)求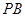 和平面
和平面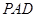 所成的角的大小;
所成的角的大小;
(Ⅱ)证明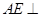 平面
平面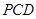 ;
;
(Ⅲ)求二面角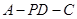 的正弦值.
的正弦值.
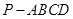 中,
中,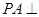 底面
底面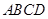 ,
,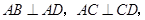
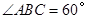 ,
,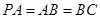 ,
,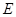 是
是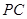 的中点.
的中点.(Ⅰ)求
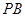 和平面
和平面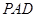 所成的角的大小;
所成的角的大小;(Ⅱ)证明
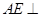 平面
平面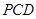 ;
;(Ⅲ)求二面角
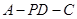 的正弦值.
的正弦值.
(Ⅰ)解:在四棱锥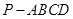 中,因
中,因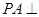 底面
底面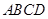 ,
,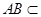 平面
平面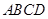 ,故
,故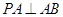 .
.
又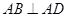 ,
,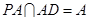 ,从而
,从而 平面
平面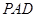 .故
.故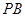 在平面
在平面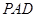 内的射影为
内的射影为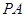 ,从而
,从而 为
为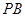 和平面
和平面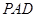 所成的角.
所成的角.
在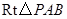 中,
中,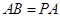 ,故
,故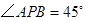 .
.
所以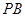 和平面
和平面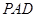 所成的角的大小为
所成的角的大小为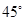 .
.
(Ⅱ)证明:在四棱锥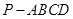 中,
中,
因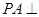 底面
底面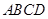 ,
,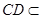 平面
平面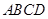 ,故
,故 .
.
由条件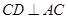 ,
,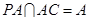 ,
,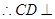 面
面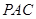 .又
.又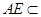 面
面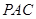 ,
,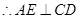 .
.
由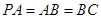 ,
,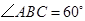 ,可得
,可得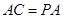 .
. 是
是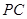 的中点,
的中点,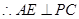 ,
,
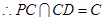 .综上得
.综上得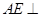 平面
平面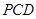 .
.
(Ⅲ)解:过点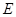 作
作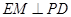 ,垂足为
,垂足为 ,连结
,连结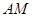 .由(Ⅱ)知,
.由(Ⅱ)知,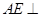 平面
平面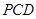 ,
,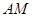 在平面
在平面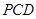 内的射影是
内的射影是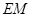 ,则
,则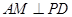 .
.
因此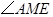 是二面角
是二面角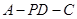 的平面角.由已知,得
的平面角.由已知,得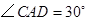 .设
.设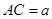 ,得
,得
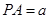 ,
,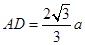 ,
,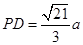 ,
,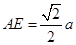 .
.
在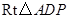 中,
中, ,
,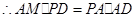 ,则
,则
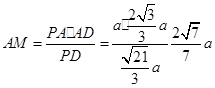 .在
.在 中,
中,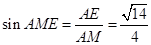 .
.
 中,因
中,因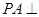 底面
底面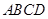 ,
,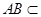 平面
平面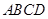 ,故
,故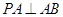 .
.
又
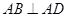 ,
,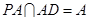 ,从而
,从而 平面
平面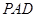 .故
.故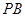 在平面
在平面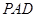 内的射影为
内的射影为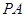 ,从而
,从而 为
为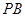 和平面
和平面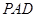 所成的角.
所成的角.在
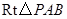 中,
中,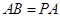 ,故
,故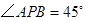 .
.所以
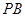 和平面
和平面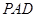 所成的角的大小为
所成的角的大小为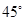 .
.(Ⅱ)证明:在四棱锥
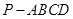 中,
中,因
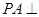 底面
底面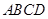 ,
,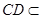 平面
平面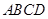 ,故
,故 .
.由条件
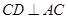 ,
,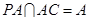 ,
,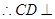 面
面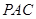 .又
.又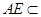 面
面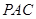 ,
,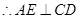 .
.由
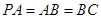 ,
,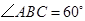 ,可得
,可得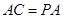 .
.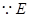 是
是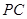 的中点,
的中点,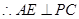 ,
,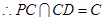 .综上得
.综上得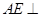 平面
平面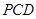 .
.(Ⅲ)解:过点
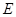 作
作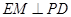 ,垂足为
,垂足为 ,连结
,连结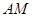 .由(Ⅱ)知,
.由(Ⅱ)知,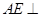 平面
平面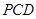 ,
,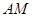 在平面
在平面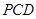 内的射影是
内的射影是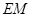 ,则
,则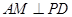 .
.因此
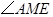 是二面角
是二面角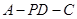 的平面角.由已知,得
的平面角.由已知,得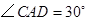 .设
.设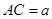 ,得
,得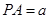 ,
,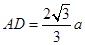 ,
,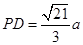 ,
,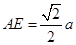 .
.在
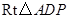 中,
中,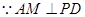 ,
,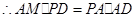 ,则
,则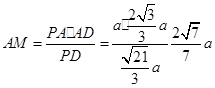 .在
.在 中,
中,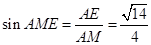 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

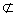 α,则a∥平面α ②a∥平面α,b
α,则a∥平面α ②a∥平面α,b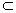 α则a∥b
α则a∥b

 中,点
中,点 分别在线段
分别在线段 上,且
上,且  .以下结论:①
.以下结论:① ;②MN//平面
;②MN//平面 ;③MN与
;③MN与 异面;④点
异面;④点 到面
到面 的距离为
的距离为 ;⑤若点
;⑤若点 与
与 确定的平面在正方体
确定的平面在正方体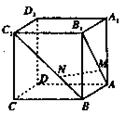
 的四个顶点都在半径为
的四个顶点都在半径为 的球面上,其中底面的三个顶点在该球的一个大圆上,球心为
的球面上,其中底面的三个顶点在该球的一个大圆上,球心为 ,
, 是线段
是线段 的中点,过
的中点,过