题目内容
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的右下顶点,且
的右下顶点,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
,![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
,![]() .
.
①若![]() ,
,![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
②若![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() .
.
【答案】(1)![]() .(2)①
.(2)①![]() ,②
,②![]() .
.
【解析】
(1)由![]() 知,
知,![]() ,又椭圆
,又椭圆![]() 过点
过点![]() ,所以将点代入椭圆方程求解即可. (2)①设直线
,所以将点代入椭圆方程求解即可. (2)①设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,与椭圆联立可求出M点坐标;又直线
,与椭圆联立可求出M点坐标;又直线![]() ,
,![]() 的斜率乘积为
的斜率乘积为![]() ,可知直线
,可知直线![]() 的方程
的方程![]() ,从而可求出N点坐标,利用
,从而可求出N点坐标,利用![]() ,
,![]() 关于
关于![]() 轴对称,列出等式
轴对称,列出等式![]() ,从而解出
,从而解出![]() 的值. (2)②利用三角形面积公式,将
的值. (2)②利用三角形面积公式,将![]() 转化为
转化为![]() ,代入点坐标计算可求出结果.
,代入点坐标计算可求出结果.
(1)由![]() 知,
知,![]() ,
,
又椭圆![]() 过点
过点![]() ,所以
,所以![]() ,
,
解得![]() 所以椭圆
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立![]()
消去![]() 并整理得,
并整理得,![]() ,
,
解得![]() ,
,![]() ,所以
,所以![]() .
.
因为直线![]() ,
,![]() 的斜率乘积为
的斜率乘积为![]() ,所以直线
,所以直线![]() 的方程
的方程![]() .
.
联立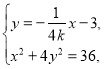 消去
消去![]() 并整理得,
并整理得,![]() ,
,
解得![]() ,
,![]() ,所以
,所以![]() .
.
①因为![]() ,
,![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
即![]() ,解得
,解得
![]() .
.
当![]() 时,点
时,点![]() 在椭圆
在椭圆![]() 外,不满足题意.
外,不满足题意.
所以直线![]() 的斜率为
的斜率为![]() .
.
②联立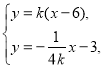 解得
解得![]() .
.
所以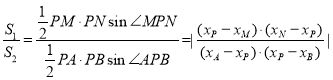
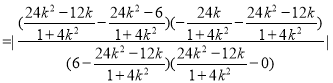
![]()
![]()
![]() .
.

【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解了近五个月的实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
销量(万量) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买新能源汽车的消费者对补贴金额的心理预期值![]() 的方差
的方差![]() 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:①回归直线的斜率和截距的最小二乘估计公式分别为: ,
,![]() ;②
;②![]() .
.
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()


