题目内容
已知函数f(x)=Asin(2x+θ),其中A≠0,θ∈(0,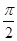 ).
).
(1)若函数f(x)的图象过点E(-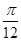 ,1),F(
,1),F(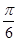 ,
,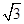 ),求函数f(x)的解析式;
),求函数f(x)的解析式;
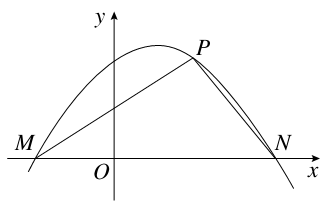
(2)如图,点M,N是函数y=f(x)的图象在y轴两侧与x轴的两个相邻交点,函数图象上一点P(t,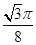 )满足
)满足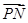 ·
·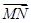 =
=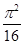 ,求函数f(x)的最大值.
,求函数f(x)的最大值.
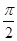 ).
).
(1)若函数f(x)的图象过点E(-
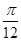 ,1),F(
,1),F(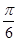 ,
,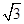 ),求函数f(x)的解析式;
),求函数f(x)的解析式;(2)如图,点M,N是函数y=f(x)的图象在y轴两侧与x轴的两个相邻交点,函数图象上一点P(t,
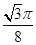 )满足
)满足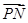 ·
·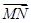 =
=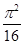 ,求函数f(x)的最大值.
,求函数f(x)的最大值.(1)f(x)=2sin(2x+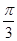 )
)
(2)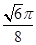
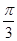 )
)(2)
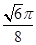
解:(1)∵函数f(x)的图象过点E(-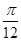 ,1),F(
,1),F(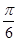 ,
,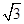 ),
),
∴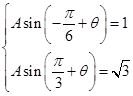 ,
,
∴sin(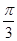 +θ)=
+θ)=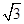 sin(-
sin(-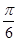 +θ),
+θ),
展开得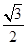 cosθ+
cosθ+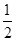 sinθ=
sinθ=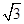 (-
(-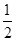 cosθ+
cosθ+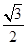 sinθ).
sinθ).
∴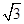 cosθ=sinθ,tanθ=
cosθ=sinθ,tanθ=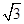 ,∵θ∈(0,
,∵θ∈(0,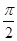 ),∴θ=
),∴θ=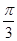 ,
,
∴f(x)=Asin(2x+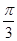 ),∵f(
),∵f(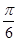 )=
)=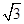 ,∴A=2.
,∴A=2.
∴f(x)=2sin(2x+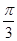 ).
).
(2)令f(x)=Asin(2x+θ)=0,
则2x+θ=kπ,k∈Z,
∵点M,N分别位于y轴的两侧,
可得M(- ,0),N(
,0),N(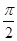 -
- ,0),
,0),
∴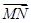 =(
=(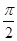 ,0),
,0),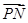 =(
=(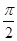 -
- -t,-
-t,-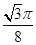 ),
),
∴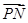 ·
·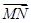 = (
= (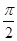 -
- -t)=
-t)=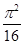 ,
,
∴ +t=
+t=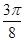 ,
,
∴θ+2t=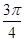 .
.
∵点P(t,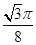 )在函数图象上,
)在函数图象上,
∴Asin(θ+2t)=Asin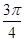 =
=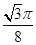 ,
,
∴A=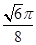 .
.
∴函数f(x)的最大值为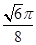 .
.
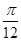 ,1),F(
,1),F(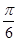 ,
,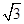 ),
),∴
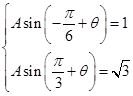 ,
,∴sin(
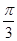 +θ)=
+θ)=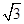 sin(-
sin(-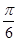 +θ),
+θ),展开得
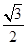 cosθ+
cosθ+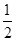 sinθ=
sinθ=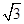 (-
(-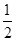 cosθ+
cosθ+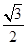 sinθ).
sinθ).∴
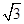 cosθ=sinθ,tanθ=
cosθ=sinθ,tanθ=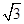 ,∵θ∈(0,
,∵θ∈(0,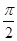 ),∴θ=
),∴θ=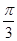 ,
,∴f(x)=Asin(2x+
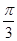 ),∵f(
),∵f(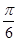 )=
)=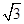 ,∴A=2.
,∴A=2.∴f(x)=2sin(2x+
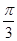 ).
).(2)令f(x)=Asin(2x+θ)=0,
则2x+θ=kπ,k∈Z,
∵点M,N分别位于y轴的两侧,
可得M(-
 ,0),N(
,0),N(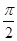 -
- ,0),
,0),∴
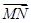 =(
=(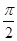 ,0),
,0),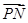 =(
=(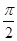 -
- -t,-
-t,-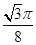 ),
),∴
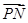 ·
·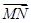 = (
= (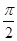 -
- -t)=
-t)=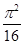 ,
,∴
 +t=
+t=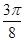 ,
,∴θ+2t=
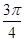 .
.∵点P(t,
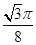 )在函数图象上,
)在函数图象上,∴Asin(θ+2t)=Asin
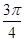 =
=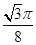 ,
,∴A=
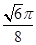 .
.∴函数f(x)的最大值为
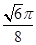 .
.
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 的图像,可将函数
的图像,可将函数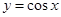 的图像向右平移
的图像向右平移 个
个 的最小值是( )
的最小值是( )



 在曲线
在曲线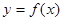 与直线
与直线 的交点中,若相邻交点距离的最小值为
的交点中,若相邻交点距离的最小值为 ,则
,则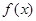 的最小正周期为( )
的最小正周期为( )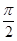



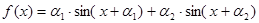 ,其中
,其中 为已知实常数,
为已知实常数, ,则下列命题中错误的是( )
,则下列命题中错误的是( ) ,则
,则 对任意实数
对任意实数 恒成立;
恒成立; ,则函数
,则函数 为奇函数;
为奇函数; ,则函数
,则函数 时,若
时,若 ,则
,则 .
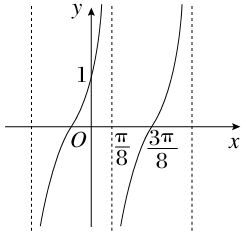
. ),y=f(x)的部分图象如图所示,则f(
),y=f(x)的部分图象如图所示,则f(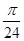 )=________.
)=________.
 ,直线x=
,直线x= 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( ) )
) ,
,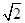 cos(
cos(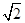 cos(-α)=-
cos(-α)=- 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若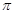 ,且当
,且当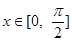 时,
时,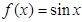 ,则
,则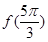 的值为
的值为



 的图象适当变化就可以得到
的图象适当变化就可以得到 的图象,这个变化可以是( )
的图象,这个变化可以是( ) 轴方向向右平移
轴方向向右平移
