题目内容
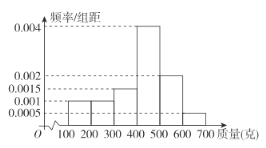
【题目】四川省双流中学是一所国家级示范高中,具有悠久的办学历史、丰富的办学经验.近年来,双中共为国内外高校输送合格新生20000余名,其中为清华、北大、复旦、人大等一流学府输送新生1800余名,上本科线人数年年超过千人,培养出省、市、县高考冠军17名,位居成都市同类学校前茅.该校高三某班有50名学生参加了今年成都市“一诊”考试,其中英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
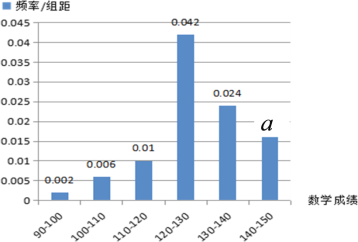
(1)如果成绩140分及以上为单科特优,则该班本次考试中英语、数学单科特优大约各多少人?
(2)试问该班本次考试中英语和数学平均成绩哪个较高,并说明理由;
(3)如果英语和数学两科都为单科特优共有5人,把(1)中的近似数作为真实值,从(1)中这些同学中随机抽取3人,设三人中英语和数学双科特优的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:
![]() 则
则
![]()
![]()
![]()
【答案】(1)英语有![]() 人,数学有
人,数学有![]() 人;(2)数学,理由见解析;(3)分布列见解析,
人;(2)数学,理由见解析;(3)分布列见解析,![]()
【解析】
(1)由英语成绩服从正态分布![]() ,求出英语成绩为单科特优的概率为
,求出英语成绩为单科特优的概率为![]() ,由此能求出英语成绩为单科特优的同学的人数,由图形先求出
,由此能求出英语成绩为单科特优的同学的人数,由图形先求出![]() ,由此能求出数学成绩特优的同学的人数;
,由此能求出数学成绩特优的同学的人数;
(2)英语的平均价成绩为120人,数学的平均成绩为127分,从而数学的平均成绩更高;
(3)英语和数学双科特优的有5人,单科特优的有8人,得到![]() 的取值为
的取值为![]() ,分别求出相应的概率,由此求得随机变量
,分别求出相应的概率,由此求得随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(1)由题意,英语成绩服从正态分布![]() ,
,
所以英语成绩为单科特优的概率为![]() ,
,
所以英语成绩为单科特优的同学约有![]() 人,
人,
因为![]() ,解得
,解得![]()
数学成绩特别优秀的同学约有![]() 人.
人.
(2)英语的平均成绩为120分,
数学的平均成绩为![]() 分,
分,
因为![]() ,所以数学的平均成绩更高.
,所以数学的平均成绩更高.
(3)英语和数学双科特优的有5人,单科特优的有8人,
从中抽取3人,随机变量![]() 可能取值有0,1,2,3,
可能取值有0,1,2,3,
![]() ;
;![]() ;
;
![]() ;
;![]()
故![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的数学期望为
的数学期望为![]() (人).
(人).

 阅读快车系列答案
阅读快车系列答案