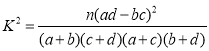题目内容
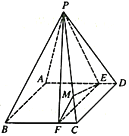
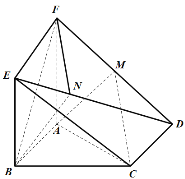
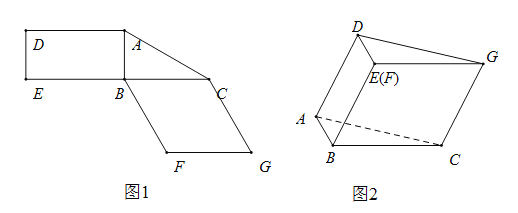
【题目】如图,在三棱柱![]() 中,
中,![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)利用面面垂直的性质定理可得![]() 平面
平面![]() ,由线面垂直的性质可得线线垂直;
,由线面垂直的性质可得线线垂直;
(2)故以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
分别求得平面![]() 与平面
与平面![]() 的法向量,利用空间向量求二面角的余弦值.
的法向量,利用空间向量求二面角的余弦值.
(1)证明:∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ;
;
(2)连接![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 为正三角形,
为正三角形,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
故以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,
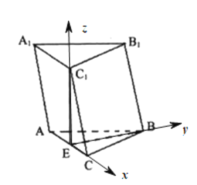
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则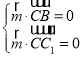 ,
,
即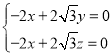 ,可取
,可取![]() ,则
,则![]() ,
,
由(1)知![]() 为平面
为平面![]() 的法向量,
的法向量,
于是![]() ,
,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]()

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案【题目】已知某种细菌的适宜生长温度为12℃~27℃,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:℃)变化的规律,收集数据如下:
(单位:℃)变化的规律,收集数据如下:
温度 | 14 | 16 | 18 | 20 | 22 | 24 | 26 |
繁殖数量 | 25 | 30 | 38 | 50 | 66 | 120 | 218 |
对数据进行初步处理后,得到了一些统计量的值,如表所示:
|
|
|
|
|
|
|
20 | 78 | 4.1 | 112 | 3.8 | 1590 | 20.5 |
其中![]() ,
,![]() .
.
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表格数据,建立![]() 关于
关于![]() 的回归方程(结果精确到0.1);
的回归方程(结果精确到0.1);
(3)当温度为27℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二成估计分别为
的斜率和截距的最小二成估计分别为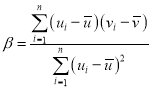 ,
,![]() ,参考数据:
,参考数据:![]() .
.
【题目】为了响应国家号召,促进垃圾分类,某校组织了高三年级学生参与了“垃圾分类,从我做起”的知识问卷作答,随机抽出男女各20名同学的问卷进行打分,作出如图所示的茎叶图,成绩大于70分的为“合格”.
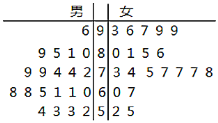
男 | 女 | 总计 | |
合格 | |||
不合格 | |||
总计 |
(1)由以上数据绘制成2×2联表,是否有95%以上的把握认为“性别”与“问卷结果”有关?
(2)从上述样本中,成绩在60分以下(不含60分)的男女学生问卷中任意选2个,求这2个学生性别不同的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |