题目内容
已知f(x)=9x-2×3x+4,x∈[-1,2].
(1)设t=3x,x∈[-1,2],求t的最大值与最小值;
(2)求f(x)的最大值与最小值.
(1)设t=3x,x∈[-1,2],求t的最大值与最小值;
(2)求f(x)的最大值与最小值.
(1)设t=3x,∵x∈[-1,2],函数t=3x在[-1,2]上是增函数,故有
≤t≤9,故t的最大值为9,t的最小值为
.
(2)由f(x)=9x-2×3x+4=t2-2t+4=(t-1)2+3,可得此二次函数的对称轴为 t=1,且
≤t≤9,
故当t=1时,函数f(x)有最小值为3,
当t=9时,函数f(x)有最大值为 67.
| 1 |
| 3 |
| 1 |
| 3 |
(2)由f(x)=9x-2×3x+4=t2-2t+4=(t-1)2+3,可得此二次函数的对称轴为 t=1,且
| 1 |
| 3 |
故当t=1时,函数f(x)有最小值为3,
当t=9时,函数f(x)有最大值为 67.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

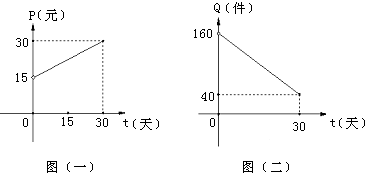
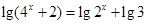 的解集为 .
的解集为 . ,且
,且 ,则
,则 ( )
( )