题目内容
【题目】在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
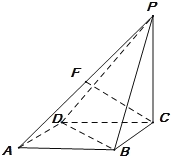
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
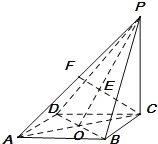
(1)连接AC,交BD于点O,连接PO,则PO与CF相交,设交点为E,则AC⊥BD,PC⊥BD,BD⊥CF,PO⊥CF,由此能证明CF⊥平面PDB;
(2)过点P作PG,使得 PG=BC,则GP∥AD∥BC,从而二面角AD-P-BC,即二面角C-PG-D,在平行四边形ADGP中,过点P作AD的垂线,垂足为H,则∠HPC即所求二面角的平面角,由此能求出平面ADP与平面BCP所成锐二面角的余弦值;
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
由于![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 与
与![]() 相交,设交点为
相交,设交点为![]() ,
,
∵底面![]() 为菱形,
为菱形,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ∴
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ∴
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
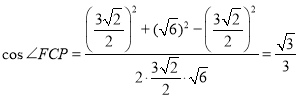 ,
,![]() ,
,
∴![]() ,又因为两个角都是锐角,
,又因为两个角都是锐角,
∴![]() ,则
,则![]() ,即
,即![]() ,
,
∵![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
(2)过点![]() 作
作![]() ,使得
,使得![]() ,
,
∵底面![]() 为菱形,
为菱形,
∴![]() ,所以二面角
,所以二面角![]() 即二面角
即二面角![]() ,
,
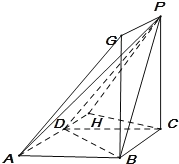
在![]() 中,过点
中,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ∴
∴![]() ,
,
∴![]() 即所求二面角的平面角,
即所求二面角的平面角,
∵![]() ,
,![]() ∴
∴![]() 平面
平面![]() ∴
∴![]()
又∵![]() ,
,![]() ∴
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,即所求二面角的平面角的余弦值为
,即所求二面角的平面角的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目