题目内容
【题目】曲线y=1+ 
与直线kx﹣y﹣2k+5=0有两个交点时，实数k的取值范围是 ．
【答案】
【解析】解：化简曲线y=1+ 
，得x2+（y﹣1）2=4（y≥1） ∴曲线表示以C（0，1）为圆心，半径r=2的圆的上半圆．
∵直线kx﹣y﹣2k+5=0可化为y﹣5=k（x﹣2），
∴直线经过定点A（2，5）且斜率为k．
又∵半圆y=1+ 与直线kx﹣y﹣2k+5=0有两个相异的交点，
∴设直线与半圆的切线为AD，半圆的左端点为B（﹣2，1），
当直线的斜率k大于AD的斜率且小于或等于AB的斜率时，
直线与半圆有两个相异的交点．
由点到直线的距离公式，当直线与半圆相切时满足 
=2，
解之得k= 
，即kAD= ．
又∵直线AB的斜率kAB=1，∴直线的斜率k的范围为k∈ ．
故答案为 ．
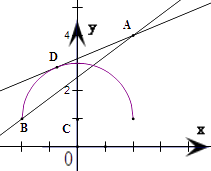
将曲线方程化简，可得曲线表示以C（0，1）为圆心、半径r=2的圆的上半圆．再将直线方程化为点斜式，可得直线经过定点A（2，5）且斜率为k．作出示意图，设直线与半圆的切线为AD，半圆的左端点为B（﹣2，1），当直线的斜率k大于AD的斜率且小于或等于AB的斜率时，直线与半圆有两个相异的交点．由此利用直线的斜率公式与点到直线的距离公式加以计算，可得实数k的取值范围．
练习册系列答案
相关题目
