题目内容
【题目】已知椭圆M: ![]() (a>b>0)的一个焦点为F(1,0),离心率为
(a>b>0)的一个焦点为F(1,0),离心率为 ![]() ,过点F的动直线交M于A,B两点,若x轴上的点P(t,0)使得∠APO=∠BPO总成立(O为坐标原点),则t=( )
,过点F的动直线交M于A,B两点,若x轴上的点P(t,0)使得∠APO=∠BPO总成立(O为坐标原点),则t=( )
A.2
B.![]()
C.![]()
D.﹣2
【答案】A
【解析】解:由题意可知c=1,椭圆的离心率e= ![]() =
= ![]() ,则a=
,则a= ![]() ,b2=a2﹣c2=1,
,b2=a2﹣c2=1,
∴椭圆的标准方程: ![]() ,
,
当直线AB斜率不存在时,t可以为任意实数,
当直线AB的斜率存在时,设AB的方程为y=k(x﹣1),设A(x1,y1),B(x1,y1),
则 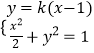 ,整理得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
,整理得:(1+2k2)x2﹣4k2x+2k2﹣2=0,
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
由∠APO=∠BPO,则直线PA与PB的斜率之和为0,
则 ![]() +
+ ![]() =0,整理得:2x1x2﹣(t+1)(x1+x2)+2t=0,
=0,整理得:2x1x2﹣(t+1)(x1+x2)+2t=0,
∴2× ![]() ﹣(t+1)×
﹣(t+1)× ![]() +2t=0,
+2t=0,
解得:t=2,
故选:A.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】已知某产品的广告费用x(单位:万元)与销售额y(单位:万元)具有线性关系关系,其统计数据如下表:
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,据此模型预报广告费用为8万元时的销售额是( )
,据此模型预报广告费用为8万元时的销售额是( )
附: ![]() =
= 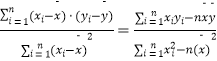 ;
; ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
A.59.5
B.52.5
C.56
D.63.5



