题目内容
(本小题满分12分)
已知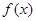 对于任意实数
对于任意实数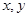 满足
满足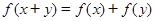 ,当
,当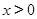 时,
时,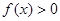 .
.
(1)求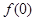 并判断
并判断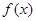 的奇偶性;
的奇偶性;
(2)判断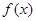 的单调性,并用定义加以证明;
的单调性,并用定义加以证明;
(3)已知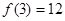 ,集合
,集合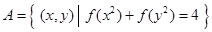 ,
,
集合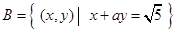 ,若
,若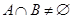 ,求实数
,求实数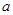 的取值范围.
的取值范围.
已知
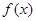 对于任意实数
对于任意实数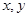 满足
满足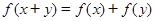 ,当
,当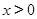 时,
时,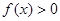 .
.(1)求
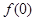 并判断
并判断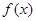 的奇偶性;
的奇偶性;(2)判断
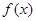 的单调性,并用定义加以证明;
的单调性,并用定义加以证明;(3)已知
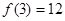 ,集合
,集合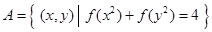 ,
,集合
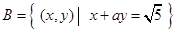 ,若
,若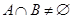 ,求实数
,求实数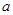 的取值范围.
的取值范围.(1)  是奇函数 (2)
是奇函数 (2) 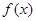 在
在 上是增函数. (3)
上是增函数. (3) 
 是奇函数 (2)
是奇函数 (2) 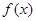 在
在 上是增函数. (3)
上是增函数. (3) 
试题分析:解:(1)令
 得
得

令
 ,得
,得

 是奇函数
是奇函数 (2)函数
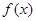 在
在 上是增函数.
上是增函数. 证明如下:
设
 ,
,  ,
,

 (或由(1)得
(或由(1)得 )
)
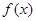 在
在 上是增函数.
上是增函数. (3)

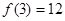 ,又
,又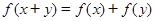 ,可得
,可得 ,
, ,
, =
=
 ,
,
 ,可得
,可得 ,
,
所以,实数
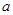 的取值范围
的取值范围 .
.点评:对于函数的奇偶性和单调性是高考考查的重点,因此要熟练的运用概念,先看定义域,然后看解析式f(x)与f(-x)的关系来确定奇偶性,同时结合抽象函数的赋值法表示来证明单调性,需要对于变量合理的变形来证明,这是一个难点,要注意积累。属于难度试题。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
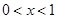 时,f(x)=x(x+1),则当
时,f(x)=x(x+1),则当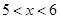 时,f(x)的表达式为
时,f(x)的表达式为 (其中常数
(其中常数 )
) 的单调性,并加以证明;
的单调性,并加以证明; 的值。
的值。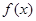 为R上的奇函数,当
为R上的奇函数,当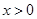 时,
时,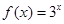 ,那么
,那么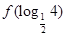 的值为 .
的值为 . 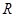 的函数
的函数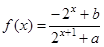 是奇函数.
是奇函数.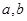 的值;
的值;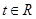 ,不等式
,不等式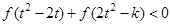 恒成立,求
恒成立,求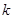 的取值范围.
的取值范围.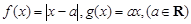 .
.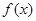 的奇偶性;(4分)
的奇偶性;(4分)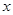 的方程
的方程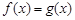 有两解,求实数
有两解,求实数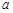 的取值范围;(6分)
的取值范围;(6分)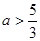 ,记
,记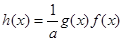 ,试求函数
,试求函数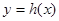 在区间
在区间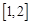 上的最大值.(10分)
上的最大值.(10分)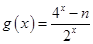 是奇函数,
是奇函数,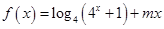 是偶函数。
是偶函数。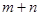 的值;
的值;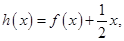 若
若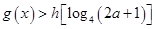 对任意
对任意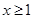 恒成立,求实数
恒成立,求实数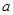 的取值范围。
的取值范围。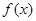 在
在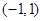 上既是奇函数,又为减函数. 若
上既是奇函数,又为减函数. 若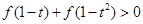 ,则
,则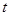 的取值范围是( )
的取值范围是( )



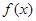 在R上单调递减,则f(-1) f(3)(用<、﹦、>填空)
在R上单调递减,则f(-1) f(3)(用<、﹦、>填空)