题目内容
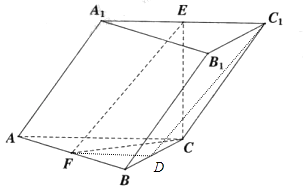
【题目】斜棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥面ABC,侧面AA1C1C为菱形,∠A1AC=60°,E,F分别为A1C1和AB的中点.
(1)求证:平面CEF⊥平面ABC;
(2)若三棱柱的所有棱长为2,求三棱柱F﹣ECB的体积;
(3)D为棱BC上一点,若C1D∥EF,请确定点D位置,并证明你的结论.
【答案】
(1)证明: ![]()
![]()
又因为侧面AA1C1C⊥面ABC,所以EC⊥CF,所以EC⊥平面ABC,
又EC在平面CEF内,所以平面CEF⊥平面ABC;
(2)解:∵CE⊥面ABC,∴CE为三棱锥E﹣BCF的高,
在Rt△CC1E中,可得 ![]() ,
,
又∵ ![]() ,
,
∴ ![]()
(3)解:D为棱BC中点点,
∵C1D∥EF,∴C1,D,E,F共面, 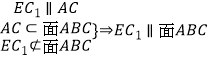
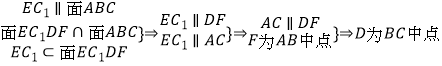 .
.
【解析】(1)根据如果一个平面经过另一平面的一条垂线,则这两个平面互相垂直;(2)三菱锥的体积为![]() 底面三角形的面积与其上高的乘积,所以确定三棱锥的高是求其体积的关键;(3)最终利用三角形中位线定理确定点D为线段BC的中点.
底面三角形的面积与其上高的乘积,所以确定三棱锥的高是求其体积的关键;(3)最终利用三角形中位线定理确定点D为线段BC的中点.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

练习册系列答案
相关题目