题目内容
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 .
,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 . 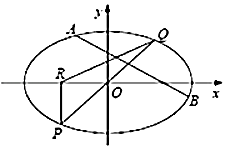
(1)若点Q的坐标为(1, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(2)求证:k1k为定值;
(3)过P点作x轴的垂线,垂足为R,若直线AB和直线QR倾斜角互补.若△PQR的面积为2 ![]() ,求椭圆C的方程.
,求椭圆C的方程.
【答案】
(1)解:由条件得: 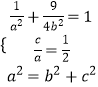 ,解得a=2,b=
,解得a=2,b= ![]() ,
,
∴椭圆方程为 ![]() =1
=1
(2)证明:设AB的中点为(x0,y0),A(x1,y1),B(x2,y2),
由于A,B为椭圆上的点,
∴ ![]() ,
, ![]() ,
,
两式相减得: ![]() +
+ ![]() =0,即
=0,即 ![]() =﹣
=﹣ ![]()
![]() =﹣
=﹣ ![]()
![]() ,
,
∵k1= ![]() ,k=
,k= ![]() ,
,
∴k1=﹣ ![]() ,即k1k=﹣
,即k1k=﹣ ![]() .
.
∵e= ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() =
= ![]() ,
,
∴k1k=﹣ ![]()
(3)解:设Q(s,t)(s>0,t>0),则P(﹣s,﹣t),R(﹣s,0),
∴kQR= ![]() =
= ![]() ,
,
∵直线AB和直线QR倾斜角互补,
∴ ![]() =﹣k1,又k1k=﹣
=﹣k1,又k1k=﹣ ![]() ,且k>0,
,且k>0,
∴k= ![]() ,
,
又S△PQR=st=2 ![]() ,
, ![]() =k=
=k= ![]() ,
,
∴s=2,t= ![]() ,即Q(2,
,即Q(2, ![]() ),
),
∴ ![]() =1,又
=1,又 ![]() ,
,
∴a=2 ![]() ,b=3,
,b=3,
∴椭圆方程为 ![]()
【解析】(1)将点Q的坐标代入椭圆方程,再根据椭圆的离心率公式e=![]() 及椭圆中a2=b2+c2,得到关于a、b、c的三个方程:(2)设出点A、点B及AB中点的坐标,然后利用”点差法“及斜率公式k=
及椭圆中a2=b2+c2,得到关于a、b、c的三个方程:(2)设出点A、点B及AB中点的坐标,然后利用”点差法“及斜率公式k=![]() 分别将k1、k用点的坐标表示出来;(3)设出点Q的坐标,根据P、Q、R三点间的位置关系将点P、点R的坐标用点Q的坐标表示出来,然后根据直线斜率公式k=
分别将k1、k用点的坐标表示出来;(3)设出点Q的坐标,根据P、Q、R三点间的位置关系将点P、点R的坐标用点Q的坐标表示出来,然后根据直线斜率公式k=![]() 将直线QR的斜率用点Q、点R的坐标表示找出k1与k的关系,与k1k=-
将直线QR的斜率用点Q、点R的坐标表示找出k1与k的关系,与k1k=-![]() 联立解出k,再将S
联立解出k,再将S![]() 用点的坐标表示并将点Q的坐标解出后代入椭圆方程.
用点的坐标表示并将点Q的坐标解出后代入椭圆方程.

【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() = (直接写出结果即可);
= (直接写出结果即可);
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.

