Question

【题目】函数 则f（﹣1）= ， 若方程f（x）=m有两个不同的实数根，则m的取值范围为

Answer 1

【答案】2﹣ ；（0，2）
【解析】解：由分段函数的表达式得f（﹣1）=| ﹣2|=2﹣ ，所以答案是：2﹣
作出函数f（x）的图像如图：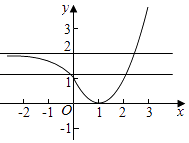

当x＜0时，f（x）=2﹣ex∈（1，2），
∴当x≤1时，f（x）∈[0，2），
当x≥1时，f（x）≥0，
若方程f（x）=m有两个不同的实数根，
则0＜m＜2，
即实数m的取值范围是（0，2），
所以答案是：2﹣ ，（0，2）．
【考点精析】关于本题考查的函数的值和函数的零点与方程根的关系，需要了解函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法；二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点才能得出正确答案．