题目内容
甲乙两人进行乒乓球比赛,各局相互独立,约定每局胜者得1分,负者得0分,如果两人比赛五局,乙得1分与得2分的概率恰好相等.
求乙在每局中获胜的概率为多少?
假设比赛进行到有一人比对方多2分或打满6局时停止,用 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 的期望
的期望 .
.
解析

练习册系列答案
相关题目
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
(1)在乙班样本中的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
附:
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程 (公里) (公里) | ||
 |  |  | |
| 纯电动乘用车 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |
 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:| 分组 | 频数 | 频率 |
 |  |  |
 |  | 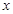 |
 |  |  |
| 合计 |  |  |
(1)求
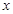 ,
, ,
, ,
, 的值;
的值;(2)若从这
 辆纯电动乘用车中任选
辆纯电动乘用车中任选 辆,求选到的
辆,求选到的 辆车续驶里程都不低于
辆车续驶里程都不低于 公里的概率;
公里的概率;(3)若以频率作为概率,设
 为购买一辆纯电动乘用车获得的补贴,求
为购买一辆纯电动乘用车获得的补贴,求 的分布列和数学期望
的分布列和数学期望 .
.  ,求
,求 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是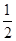 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
 ,求
,求 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.