题目内容
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
(1)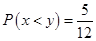 (2)
(2)
解析试题分析:该问题属古典概型,甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y,有36个基本事件,每个基本事件发生的概率都相等,且互斥;(1)统计出事件“x<y”所包含的基本事件的个数进而求出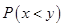
(2)统计出事件“5<x+y<10”所包含的基本事件的个数进而求出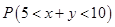
解:记基本事件为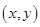 ,则有
,则有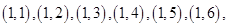
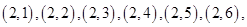
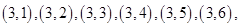
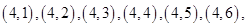
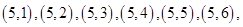
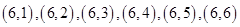
共36个基本事件
其中满足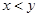 的基本事件有
的基本事件有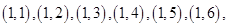
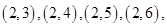
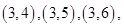
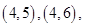
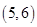
共15个.
满足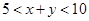 的基本事件有
的基本事件有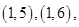
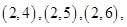
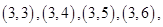
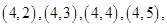
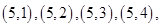
 共20个.
共20个.
(1)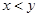 的概率
的概率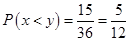
(2)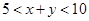 的概率
的概率
考点:古典概率

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P1 | P2 | P3 | P4 |
(1)求q2的值;
(2)求随机变量ξ的数学期望E(ξ);
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和数学期望;
(2)根据以上数据,我们能否在犯错误的概率不超过0.01的前提下,认为“在20:00-22:00时间段居民的休闲方式与性别有关系”?
参考公式:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。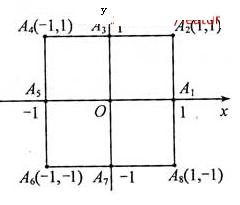
 表示比赛停止时已打局数,求
表示比赛停止时已打局数,求 .
.