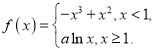题目内容
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,且底面
,且底面![]() 为边长为2的菱形,
为边长为2的菱形,
![]() ,
,![]()
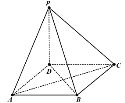
(1)证明:面![]() 面
面![]() ;
;
(2)在图中作出点![]() 在平面
在平面![]() 内的正投影
内的正投影![]() (说明作法及其理由),并求四面体
(说明作法及其理由),并求四面体![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)由菱形得![]() ,又由已知线面垂直,得
,又由已知线面垂直,得![]() ,从而可证得
,从而可证得![]() 平面
平面![]() ,从而证得面面垂直.
,从而证得面面垂直.
(2)考虑到已知可得![]() ,从而应该有
,从而应该有![]() ,因此再由底面菱形中有内角为60°可得作法:只要取BC中点E,连接PE,在平面DEP内作DM⊥PE于M即可.得出M点位置后可计算四面体体积.
,因此再由底面菱形中有内角为60°可得作法:只要取BC中点E,连接PE,在平面DEP内作DM⊥PE于M即可.得出M点位置后可计算四面体体积.
详解:(1)因为![]() 平面
平面![]() ,
,![]() ,所以
,所以![]()
在菱形![]() 中,
中,![]() ,且
,且![]() ,
,
所以![]()
又因为![]() ,所以面
,所以面![]() 面
面![]()
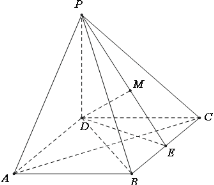
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,易得
,易得![]() 是等边三角形,
是等边三角形,
所以![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]()
在面![]() 中,过
中,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() 是点
是点![]() 在平面
在平面![]() 内的正投影
内的正投影
经计算得![]() ,在
,在![]() 中,
中,![]() ,
,![]()
![]() ,
,![]()
![]()

练习册系列答案
相关题目
【题目】某人群中各种血型的人所占的比例见下表:
血腥 | A | B | AB | O |
该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血,O型血可以给任一种血型的人输血,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.该人群中的小明是B型血,若他因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?