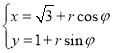题目内容
【题目】已知实数a>0且a≠1.设命题p:函数f(x)=logax在定义域内单调递减;命题q:函数g(x)=x2﹣2ax+1在(![]() ,+∞)上为增函数,若“p∧q”为假,“p∨q”为真,求实数a的取值范围.
,+∞)上为增函数,若“p∧q”为假,“p∨q”为真,求实数a的取值范围.
【答案】![]()
【解析】
先分别求得p,q为真时的a的范围,再将问题转化为p,q一真一假时,分类讨论可得答案.
∵函数f(x)=logax在定义域内单调递减,∴0<a<1.
即:p:{a|0<a<1}.
∵a>0且a≠1,∴¬p:{a|a>1},
∵g(x)=x2﹣2ax+1在(![]() ,+∞)上为增函数,∴a
,+∞)上为增函数,∴a![]() .
.
又∵a>0且a≠1,
即q:{a|0<a![]() }.
}.
∴¬q:{a|a![]() 且a≠1}.
且a≠1}.
又∵“p∧q”为假,“p∨q”为真,∴“p真q假”或“p假q真”.
①当p真q假时,{a|0<a<1}∩{a|a![]() 且a≠1}={a|
且a≠1}={a|![]() a<1}..
a<1}..
②当p假q真时,{a|a>1}∩{a|0<a![]() }=,
}=,
综上所述:实数a的取值范围是:{a|![]() a<1}.
a<1}.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.