题目内容
给出下列等式:①an+1-an=p(p为常数,n∈N*);②2an+1=an+an+2(n∈N*);③an=kn+b(k,b为常数,n∈N*),则以上可以判断无穷数列{an}为等差数列的是______(写序号即可)
对于①,由an+1-an=p,符合等差数列的定义,故可以判定数列{an}是等差数列;
对于②,由2an+1=an+an+2(n∈N*),则an+2-an+1=an+1-an,即数列中的任意后一项减前一项都等于同一个常数,符合等差数列的定义,故可以判定数列{an}是等差数列;
对于③,由an=kn+b(k,b为常数,n∈N*),则an+1-an=k(n+1)-b-(kn+b)=k为常数,符合等差数列的定义,故可以判定数列{an}是等差数列.
综上所述,可以判断无穷数列{an}为等差数列的是①②③.
故答案为:①②③.
对于②,由2an+1=an+an+2(n∈N*),则an+2-an+1=an+1-an,即数列中的任意后一项减前一项都等于同一个常数,符合等差数列的定义,故可以判定数列{an}是等差数列;
对于③,由an=kn+b(k,b为常数,n∈N*),则an+1-an=k(n+1)-b-(kn+b)=k为常数,符合等差数列的定义,故可以判定数列{an}是等差数列.
综上所述,可以判断无穷数列{an}为等差数列的是①②③.
故答案为:①②③.

练习册系列答案
相关题目
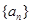 为等比数列,
为等比数列,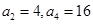 ,记
,记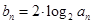 .
.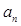 和
和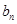 ;
;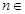
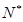 ,有
,有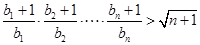 成立.
成立.