题目内容
在数列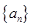 中,
中,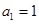 ,
, ,
, 对任意
对任意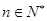 成立,令
成立,令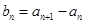 ,且
,且 是等比数列.
是等比数列.
(1)求实数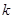 的值;
的值;
(2)求数列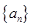 的通项公式;
的通项公式;
(3)求证: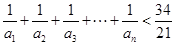 .
.
(1)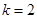 ;(2)
;(2)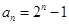 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)先利用题中的定义,利用数列 的前三项成等比数列求出
的前三项成等比数列求出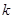 的值,然后就
的值,然后就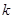 的值进行检验,即对数列
的值进行检验,即对数列 是否为等比数列进行检验;(2)根据等比数列
是否为等比数列进行检验;(2)根据等比数列 的通项
的通项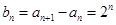 选择累加法求数列
选择累加法求数列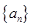 的通项公式;(3)利用
的通项公式;(3)利用 ,将数列
,将数列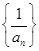 从第三项开始放缩为一个等比数列,而前面两项的值保持不变,再利用数列求和即可证明相应的数列不等式.
从第三项开始放缩为一个等比数列,而前面两项的值保持不变,再利用数列求和即可证明相应的数列不等式.
试题解析:(1)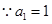 ,
, ,
,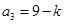 ,
,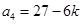 ,
,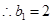 ,
,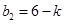 ,
,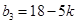 ,
,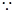 数列
数列 为等比数列,
为等比数列,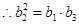 ,即
,即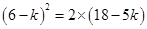 ,解得
,解得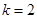 或
或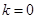 (舍),
(舍),
当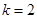 时,
时,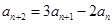 ,即
,即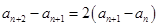 ,
,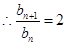 ,所以
,所以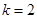 满足条件;
满足条件;
(2) ,数列
,数列 为等比数列,
为等比数列,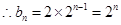 ,
,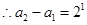 ,
,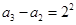 ,
,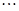 ,
, ,
, ,
,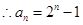 ;
;
(3) ,
,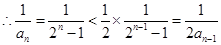 ,
,
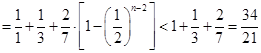 .
.
考点:1.等比数列的定义;2.累加法求数列的通项公式;3.放缩法

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
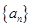 的前
的前 项和为
项和为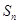 ,若
,若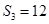 ,且
,且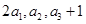 成等比数列.
成等比数列.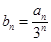 的前
的前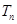 ,求
,求 的前
的前 项和为
项和为 .且
.且 .
. ,数列
,数列 满足:
满足:

 ,求数列
,求数列 的前
的前 项和
项和 .
.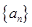 的前
的前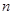 项和为
项和为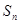 ,公差
,公差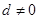 ,
,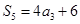 ,且
,且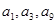 成等比数列.
成等比数列.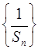 的前
的前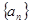 是等差数列,且
是等差数列,且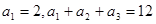
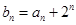 ,求数列
,求数列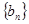 前n项和
前n项和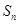 .
.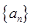 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*. 为何值时,数列
为何值时,数列 是数列
是数列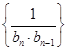 的前
的前 项和,求
项和,求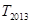 的值.
的值. 满足:
满足: ,
, .
. 及
及 ,求数列
,求数列 的前n项和
的前n项和 .
. 是正数列组成的数列,
是正数列组成的数列, ,且点
,且点 在函数
在函数 的图像上,
的图像上, 满足
满足 ,
, ,求证:
,求证: .
.