题目内容
已知正项等差数列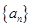 的前
的前 项和为
项和为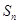 ,若
,若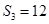 ,且
,且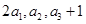 成等比数列.
成等比数列.
(Ⅰ)求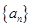 的通项公式;
的通项公式;
(Ⅱ)记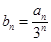 的前
的前 项和为
项和为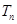 ,求
,求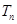 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)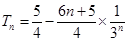
解析试题分析:(Ⅰ)由 和
和 可得
可得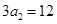 ,即
,即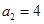 ;又
;又 ,
,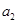 ,
,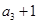 成等比数列,得
成等比数列,得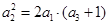 ,综合起来可求得
,综合起来可求得 即可.(Ⅱ)由已知可求出
即可.(Ⅱ)由已知可求出 ,即数列{
,即数列{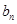 }是由等差数列和等比数列组合而成,前
}是由等差数列和等比数列组合而成,前 项和为
项和为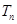 可由错位相减法求得.
可由错位相减法求得.
试题解析:(Ⅰ)∵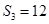 ,即
,即 ,∴
,∴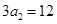 ,所以
,所以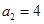 , 2分
, 2分
又∵ ,
,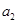 ,
,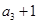 成等比数列,
成等比数列,
∴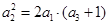 ,即
,即 , 4分
, 4分
解得, 或
或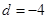 (舍去),
(舍去),
∴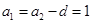 ,故
,故 ; 6分
; 6分
(Ⅱ)法1:  ,
,
∴ , ①
, ①
①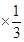 得,
得, ②
②
①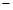 ②得,
②得,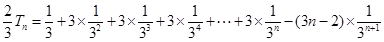
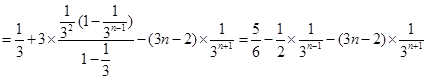
∴ . 12分
. 12分
考点:1.等差数列和等比数列的性质;2. 求数列前n项和.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且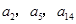 分别是等比数列{
分别是等比数列{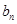 }的b2,b3,b4.
}的b2,b3,b4.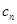 }对任意自然数n均有
}对任意自然数n均有 成立,求
成立,求 的值.
的值. 中,
中,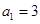 ,
, ,
,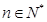 .
. 是等比数列,并求数列
是等比数列,并求数列 且
且 ,
,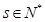 ,求证:使得
,求证:使得 ,
,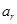 ,
, 成等差数列的点列
成等差数列的点列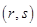 在某一直线上.
在某一直线上.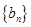 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列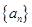 的前n项和
的前n项和 .
. , 求数列
, 求数列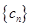 的前n项和
的前n项和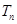 .
. 的集合:①对任意
的集合:①对任意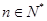 ,
,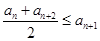 恒成立;②对任意
恒成立;②对任意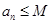 恒成立.
恒成立.
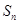 是其前n项和,且
是其前n项和,且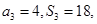 试探究数列
试探究数列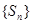 与集合W之间的关系;
与集合W之间的关系; 的通项公式为
的通项公式为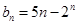 ,且
,且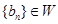 ,求M的取值范围.
,求M的取值范围. 、
、 满足
满足 ,且
,且 ,其中
,其中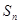 为数列
为数列 项和,又
项和,又 ,对任意
,对任意 都成立。
都成立。 的前
的前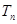
 中,
中,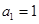 ,
, ,数列
,数列 中,
中,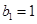 ,且点
,且点 在直线
在直线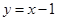 上.
上.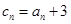 ,求数列
,求数列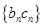 的前项和
的前项和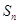 .
. 的方程为
的方程为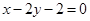 ,数列
,数列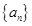 满足
满足 ,其前
,其前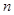 项和为
项和为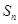 ,点
,点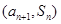 在直线
在直线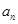 和
和 之间插入
之间插入 个数组成公差为
个数组成公差为 的等差数列,令
的等差数列,令 ,试证明
,试证明 .
. 中,
中,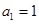 ,
, ,
, 对任意
对任意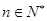 成立,令
成立,令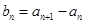 ,且
,且 是等比数列.
是等比数列.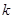 的值;
的值;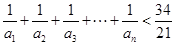 .
.