题目内容
某公司生产某种产品的固定成本为150万元,而每生产x千件产品每年需另增加的可变成本为C(x)(单位:万元),且C(x)=
,每件产品的售价为500元,且假定该公司生产的产品能全部售出.
(Ⅰ)写出年利润L(x)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司所获利润最大?最大利润是多少?
|
(Ⅰ)写出年利润L(x)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司所获利润最大?最大利润是多少?
考点:分段函数的应用
专题:函数的性质及应用
分析:(Ⅰ)根据条件即可建立年利润L(x)关于年产量x(千件)的函数解析式;
(Ⅱ)根据函数的表达式,利用基本不等式即可求出最大值.
(Ⅱ)根据函数的表达式,利用基本不等式即可求出最大值.
解答:解:(Ⅰ)当0<x<80,x∈N*时,L(x)=
-(
x2+10x)-150=-
x2+40x-150;
当x≥80,x∈N*时,L(x)=
-(51x+
)-1450-150=1300-(x+
).
则L(x)=
.
(Ⅱ)当0<x<80,x∈N*时,L(x)=-
(x-60)2+40x+1050.
∴当x=60时,L(x)取得最大值L(60)=1050.
当x≥80,x∈N*时,L(x)=1300-(x+
)≤1300-2
=1100.
∴当x=
,即x=100时,L(x)取得最大值L(100)=1100.
综上,当x=100时,L(x)取得最大值1100,即年产量为100千件时,该公司所获利润最大.
| 500×1000x |
| 10000 |
| 1 |
| 3 |
| 1 |
| 3 |
当x≥80,x∈N*时,L(x)=
| 500×1000x |
| 10000 |
| 10000 |
| x |
| 10000 |
| x |
则L(x)=
|
(Ⅱ)当0<x<80,x∈N*时,L(x)=-
| 1 |
| 3 |
∴当x=60时,L(x)取得最大值L(60)=1050.
当x≥80,x∈N*时,L(x)=1300-(x+
| 10000 |
| x |
x•
|
∴当x=
| 10000 |
| x |
综上,当x=100时,L(x)取得最大值1100,即年产量为100千件时,该公司所获利润最大.
点评:本题主要考查函数的应用,以及函数最值的求解,利用基本不等式的性质是解决本题的关键.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
已知函数f(x)=x2014(x∈R),又α、β是锐角三角形的两个内角,则有( )
| A、f(sinα)>f(cosβ) | B、f(sinα)<f(cosβ) | C、f(sinα)>f(sinβ) | D、f(cosα)>f(cosβ) |
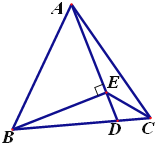 如图,△ABC是边长为2的等边三角形,D是边BC上的动点,BE⊥AD于E,则CE的最小值为( )
如图,△ABC是边长为2的等边三角形,D是边BC上的动点,BE⊥AD于E,则CE的最小值为( )| A、1 | ||||
B、2-
| ||||
C、
| ||||
D、
|
三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )


A、2
| ||
B、4
| ||
C、
| ||
D、16
|
已知平面α、β和直线m,给出条件:①m∥α;②m⊥α;③m?α;④α⊥β;⑤α∥β.由这五个条件中的两个同时成立能推导出m∥β的是( )
| A、①④ | B、①⑤ | C、②⑤ | D、③⑤ |
某程序框图如图所示,若输入x=
,则该程序运行后输出的a,b值分别是( )

| π |
| 2 |

| A、0,1 | B、1,1 |
| C、1,0 | D、0,0 |