题目内容
下列推理是归纳推理的是（ ）
Ａ．A，B为定点，动点P满足|PA|＋|PB|＝2a＞|AB|，则P点的轨迹为椭圆
B．由
，求出
猜想出数列的前n项和Sn的表达式
Ｃ．由圆
的面积
，猜想出椭圆
的面积
D．科学家利用鱼的沉浮原理制造潜艇
B
解析试题分析：根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理，叫做归纳推理（简称归纳）.由A可知其为椭圆的定义；B由求出猜想出数列的前n项和Sn的表达式,属于归纳推理；C由圆的面积，猜想出椭圆的面积,是类比推理；D科学家利用鱼的沉浮原理制造潜艇，也属于类比推理，故选B.
考点：归纳推理
练习册系列答案
相关题目
已知数列{an}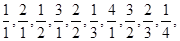
…，依它的10项的规律，则a99+a100的值为（ ）
A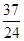． | B． | C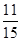． | D． |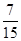
观察式子：1＋
<
，1＋＋
<
，1＋＋＋
<
， ，则可归纳出一般式子为( )
A．1＋＋＋ ＋ < (n≥2) | B．1＋＋＋ ＋< (n≥2) |
C．1＋＋＋ ＋< (n≥2) | D．1＋＋＋ ＋< (n≥2) |
仔细观察下面○和●的排列规律：
○●○○●○○○●○○○○●○○○○○●○○○○○○ ●……
若依此规律继续下去，得到一系列的○和●，那么在前120个○和●中，●的个数是（ ）
| A．13 | B．14 | C．15 | D．16 |
在数列{an}中，an＝1－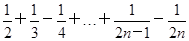
则ak＋1＝( )．
A．ak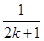＋ | B．ak＋ － |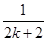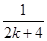
| C．ak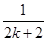＋ | D．ak＋－ |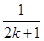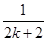
下列表述正确的是 ( )
①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理．
| A．①②③ | B．②③④ |
| C．②④⑤ | D．①③⑤ |
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
| A．18 | B．36 | C．48 | D．54 |
推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是( )
| A．① | B．② |
| C．③ | D．以上均错 |