题目内容
在数列{an}中,an=1-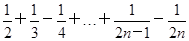 则ak+1=( ).
则ak+1=( ).
A.ak+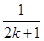 | B.ak+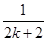 - -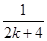 |
C.ak+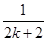 | D.ak+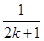 - -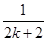 |
D
解析

练习册系列答案
相关题目
用反证法证明某命题时,对其结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证 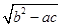 <
<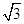 a”索的因应是( )
a”索的因应是( )
| A.a-b>0 | B.a-c>0 |
| C.(a-b)(a-c)>0 | D.(a-b)(a-c)<0 |
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
| A.28 | B.76 | C.123 | D.199 |
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |
某个命题与正整数有关,如果当n=k(k∈N+)时,该命题成立,那么可
推得当n=k+1时命题也成立.现在已知当n=5时,该命题不成立,那么可推得( ).
| A.当n=6时该命题不成立 |
| B.当n=6时该命题成立 |
| C.当n=4时该命题不成立 |
| D.当n=4时该命题成立 |
下面几种推理过程是演绎推理的是( )
| A.某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人 |
| B.由三角形的性质,推测空间四面体的性质 |
| C.平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分 |
D.在数列{an}中,a1=1,an=  ,由此归纳出{an}的通项公式 ,由此归纳出{an}的通项公式 |
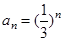 ,把数列
,把数列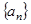 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,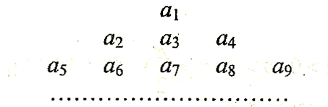
 表示第
表示第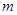 行的第
行的第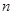 个数,则
个数,则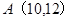 = ( )
= ( )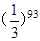

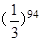
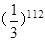
 ,求出
,求出 猜想出数列的前n项和Sn的表达式
猜想出数列的前n项和Sn的表达式 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 的面积
的面积