题目内容
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
按照以上排列的规律,第n 行(n ≥3)从左向右的第3 个数为 __.
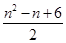
解析试题分析:前n-1行共有正整数1+2+…+(n-1)个,即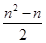 个,
个,
因此第n行第3个数是全体正整数中第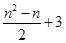 个,即为
个,即为 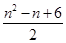 .
.
考点:归纳推理.

练习册系列答案
相关题目
用反证法证明某命题时,对其结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是( )
| A.21 | B.28 | C.32 | D.36 |
用演绎法证明函数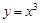 是增函数时的小前提是 ( )
是增函数时的小前提是 ( )
| A.增函数的定义 | B.函数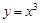 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则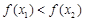 | D.若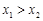 ,则 ,则 |
现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是 的正方形,其中一个的某顶点在另一个的中心,则这两个正
的正方形,其中一个的某顶点在另一个的中心,则这两个正
|
 ;类比到空间,有两个棱长均为
;类比到空间,有两个棱长均为 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为___________ .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为___________ .
 ,求出
,求出 猜想出数列的前n项和Sn的表达式
猜想出数列的前n项和Sn的表达式 的面积
的面积 ,猜想出椭圆
,猜想出椭圆 的面积
的面积
 ,则得分点C的坐标公式
,则得分点C的坐标公式 ,对于函数
,对于函数 上任意两点
上任意两点 ,
, ,线段AB必在弧AB上方.由图象中的点C在点C′正上方,有不等式
,线段AB必在弧AB上方.由图象中的点C在点C′正上方,有不等式 成立.对于函数
成立.对于函数 的图象上任意两点
的图象上任意两点 ,
, ,类比上述不等式可以得到的不等式是_________ .
,类比上述不等式可以得到的不等式是_________ . ,第
,第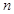 个三角形数为
个三角形数为 .记第
.记第 边形数为
边形数为 (
( ),以下列出了部分
),以下列出了部分 正方形数
正方形数 
 六边形数
六边形数 
 .
. ,且
,且 当
当 且
且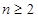 时,
时, 猜想
猜想 的表达式 .
的表达式 .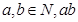 能被3整除,那么
能被3整除,那么 中至少有一个能被3整除"时,假设应为 .
中至少有一个能被3整除"时,假设应为 .