题目内容
过点M(0,1)作直线,使它被两已知直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M所平分,求此直线方程.
直线方程为x+4y-4=0.
本题中最重要的已知条件是M为所截得线段的中点,用好这个条件是解题的关键.
解法一:过点M与x轴垂直的直线显然不合要求,故设直线方程y=kx+1,若与两已知直线分别交于A、B两点,则解方程组可得
xA= ,xB=
,xB=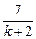 .
.
由题意 +
+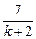 =0,
=0,
∴k=- .故直线方程为x+4y-4=0.
.故直线方程为x+4y-4=0.
解法二:设所求直线方程y=kx+1,
代入方程(x-3y+10)(2x+y-8)=0,
得(2-5k-3k2)x2+(28k+7)x-49=0.
由xA+xB=-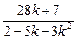 =2xM=0,解得k=-
=2xM=0,解得k=- .
.
∴直线方程为x+4y-4=0.
解法三:∵点B在直线2x-y-8=0上,故可设B(t,8-2t),由中点公式得A(-t,2t-6).
∵点A在直线x-3y+10=0上,
∴(-t)-3(2t-6)+10=0,得t=4.∴B(4,0).故直线方程为x+4y-4=0.
解法一:过点M与x轴垂直的直线显然不合要求,故设直线方程y=kx+1,若与两已知直线分别交于A、B两点,则解方程组可得
xA=
 ,xB=
,xB=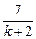 .
.由题意
 +
+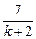 =0,
=0,∴k=-
 .故直线方程为x+4y-4=0.
.故直线方程为x+4y-4=0.解法二:设所求直线方程y=kx+1,
代入方程(x-3y+10)(2x+y-8)=0,
得(2-5k-3k2)x2+(28k+7)x-49=0.
由xA+xB=-
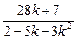 =2xM=0,解得k=-
=2xM=0,解得k=- .
.∴直线方程为x+4y-4=0.
解法三:∵点B在直线2x-y-8=0上,故可设B(t,8-2t),由中点公式得A(-t,2t-6).
∵点A在直线x-3y+10=0上,
∴(-t)-3(2t-6)+10=0,得t=4.∴B(4,0).故直线方程为x+4y-4=0.

练习册系列答案
相关题目
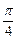 后,所得的直线方程是
后,所得的直线方程是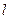 在
在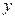 轴上的截距为
轴上的截距为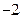 ,直线
,直线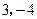 的两点的线段长为
的两点的线段长为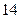 ,求直线
,求直线 过点
过点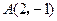 ,倾斜角
,倾斜角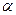 的范围是
的范围是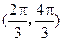 .在直角坐标系中给定两点
.在直角坐标系中给定两点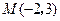 ,
,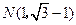 ,问
,问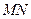 是否有交点?若有交点,请说明理由.
是否有交点?若有交点,请说明理由.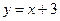 与曲线
与曲线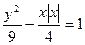 的交点的个数是 个.
的交点的个数是 个.