题目内容
【题目】（本小题满分13分）
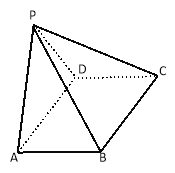
如图，在正四面体
中，
分别是棱
的中点.
（1）求证：四边形
是平行四边形；
（2）求证：
平面；
（3）求证：
平面
.
【答案】见解析.
【解析】
试题分析：第一问应用三角形的中位线的性质，可知四边形的一组对边平行且相等的，从而根据平行四边形的判定定理，得出结果，对于第二问，注意把握线面平行的判定定理的内容，找准平行线即可，三角形的中位线是现成的，对于第三问，掌握线面垂直的判定定理的内容，找准两条相交直线与之垂直即可，正三角形的中线和垂线是重合的，好好写即可.
试题解析：
证明：（1）∵
分别是棱
的中点，
∴
，且
， （2分）
∴
且
， （3分）
∴四边形
是平行四边形. （4分）
（2）由（1）知，
， （5分）
且
平面，
平面， （7分）
∴
平面. （8分）
（3）∵
是正四面体，
所以它的四个面是全等的等边三角形. （9分）
∵ H是BC的中点，
∴
. （11分）
又SH平面SAH，AH平面SAH，且
，（12分）
∴
平面
. （13分）
练习册系列答案
相关题目
