题目内容
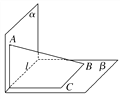
【题目】四棱锥P﹣ABCD中，底面ABCD是边长为8的菱形，∠BAD=
，若PA=PD=5，平面PAD⊥平面ABCD．
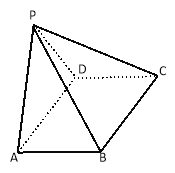
（1）求四棱锥P﹣ABCD的体积；
（2）求证：AD⊥PB．
【答案】（1）
（2）详见解析
【解析】
试题分析：（1）过P作PM⊥AD于M．利用面PAD⊥面ABCD可得PM⊥面ABCD，菱形ABCD的面积
，再利用
即可得出；（2）连接BM．利用BD=BA=8，AM=DM，
．可得AD⊥BM，又AD⊥PM，可得AD⊥平面PMB，即可得出
试题解析：（1）过P作PM⊥AD于M．∵面PAD⊥面ABCD，面PAD∩面ABCD=AD，PM面PAD．
∴PM⊥面ABCD，
又PA=PD=5，AD=8．
∴M为AD的中点且PM=
=3．
∵
，AD=8，
∴菱形ABCD的面积S=
=
．
∴VP﹣ABCD=
=
=
．
（2）证明：连接BM．
∵BD=BA=8，AM=DM，
．
∴AD⊥BM，
又AD⊥PM，且BM∩PM=M．
∴AD⊥平面PMB．
∴AD⊥PB．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
