题目内容
设集合 数列
数列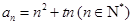 单调递增
单调递增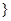 ,集合
,集合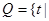 函数
函数 在区间
在区间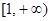 上单调递增
上单调递增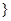 ,若“
,若“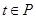 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数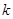 的最小值为 .
的最小值为 .
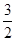
解析试题分析:由数列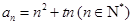 单调递增得:
单调递增得: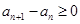 对
对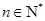 恒成立,即
恒成立,即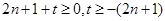 对
对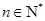 恒成立,所以
恒成立,所以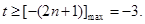 由函数
由函数 在区间
在区间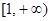 上单调递增得:
上单调递增得: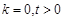 或
或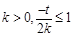 .因为“
.因为“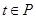 ”是“
”是“ ”的充分不必要条件,所以
”的充分不必要条件,所以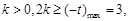 即
即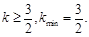
考点:数列单调性,二次函数单调性,不等式恒成立

练习册系列答案
相关题目
题目内容
设集合 数列
数列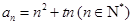 单调递增
单调递增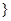 ,集合
,集合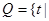 函数
函数 在区间
在区间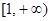 上单调递增
上单调递增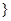 ,若“
,若“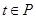 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数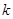 的最小值为 .
的最小值为 .
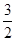
解析试题分析:由数列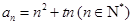 单调递增得:
单调递增得: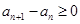 对
对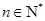 恒成立,即
恒成立,即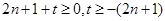 对
对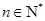 恒成立,所以
恒成立,所以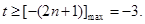 由函数
由函数 在区间
在区间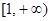 上单调递增得:
上单调递增得: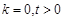 或
或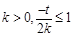 .因为“
.因为“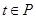 ”是“
”是“ ”的充分不必要条件,所以
”的充分不必要条件,所以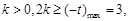 即
即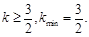
考点:数列单调性,二次函数单调性,不等式恒成立
