题目内容
如图,在四棱锥P-ABCD中,底面ABCD是矩形,
PA⊥底面ABCD,E是PC的中点.已知AB=2,
AD=2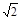 ,PA=2.求:
,PA=2.求:
(1)三角形PCD的面积;(6分)
(2)异面直线BC与AE所成的角的大小.(6分)
PA⊥底面ABCD,E是PC的中点.已知AB=2,
AD=2
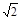 ,PA=2.求:
,PA=2.求:(1)三角形PCD的面积;(6分)
(2)异面直线BC与AE所成的角的大小.(6分)

(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.解:(1)因为PA⊥底面ABCD,所以PA⊥CD,又AD⊥CD,所以CD⊥平面PAD,
从而CD⊥PD. ……3分

因为PD= ,CD=2,所以三角形PCD的面积为
,CD=2,所以三角形PCD的面积为 .
.
……6分
(2)[解法一]如图所示,建立空间直角坐标系,则B(2, 0, 0),C(2, 2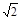 ,0),E(1,
,0),E(1, 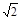 , 1),
, 1),
 ,
, . ……8分
. ……8分
设 与
与 的夹角为q,则
的夹角为q,则 ,q=
,q= .
.

由此可知,异面直线BC与AE所成的角的大小是 ……12分
……12分
[解法二]取PB中点F,连接EF、AF,则EF∥BC,从而∠AEF(或其补角)是异面直线
BC与AE所成的角 ……8分
在 中,由EF=
中,由EF=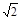 、AF=
、AF=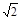 、AE=2,知
、AE=2,知 是等腰直角三角形,所以∠AEF=
是等腰直角三角形,所以∠AEF= .
.
因此异面直线BC与AE所成的角的大小是 ……12分
……12分
从而CD⊥PD. ……3分

因为PD=
 ,CD=2,所以三角形PCD的面积为
,CD=2,所以三角形PCD的面积为 .
. ……6分
(2)[解法一]如图所示,建立空间直角坐标系,则B(2, 0, 0),C(2, 2
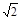 ,0),E(1,
,0),E(1, 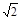 , 1),
, 1), ,
, . ……8分
. ……8分设
 与
与 的夹角为q,则
的夹角为q,则 ,q=
,q= .
.
由此可知,异面直线BC与AE所成的角的大小是
 ……12分
……12分[解法二]取PB中点F,连接EF、AF,则EF∥BC,从而∠AEF(或其补角)是异面直线
BC与AE所成的角 ……8分
在
 中,由EF=
中,由EF=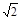 、AF=
、AF=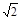 、AE=2,知
、AE=2,知 是等腰直角三角形,所以∠AEF=
是等腰直角三角形,所以∠AEF= .
. 因此异面直线BC与AE所成的角的大小是
 ……12分
……12分
练习册系列答案
相关题目
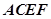 所在平面与矩形
所在平面与矩形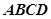 所在平面垂直,
所在平面垂直,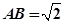 ,
,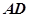 =1,
=1,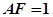 ,
,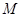 是线段
是线段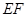 的中点.
的中点.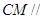 平面
平面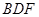 ;
;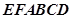 的表面积;
的表面积;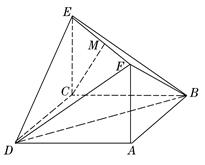
 中,四边形
中,四边形 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
. ;
; 为线段
为线段 的中点,求证:
的中点,求证: ;
; ,且二面角
,且二面角 的大小为
的大小为 ,
, 的体积.
的体积. 

 ,OC=
,OC= ,则三棱锥O-ABC外接球的表面积为( )
,则三棱锥O-ABC外接球的表面积为( ) 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边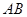 、
、 上,且
上,且 ,
, ,将此正方形沿
,将此正方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥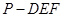 的体积是
的体积是







 中,
中,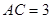 ,
,  ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
; 的体积.
的体积.

 ,则此圆柱的母线长为( )
,则此圆柱的母线长为( )