题目内容
【题目】圆C过点A（6，4），B（1，﹣1），且圆心在直线l：x﹣5y+7=0上．
（1）求圆C的方程；
（2）P为圆C上的任意一点，定点Q（7，0），求线段PQ中点M的轨迹方程．
【答案】
（1）解：设所求圆的方程为（x﹣a）2+（y﹣b）2=r2．由题意得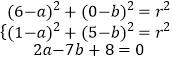 
解得a=3，b=2，r= 
所以所求圆的方程是（x﹣3）2+（y﹣2）2=13
（2）解：设线段PQ的中点M（x，y），P（x0，y0）
M为线段PQ的中点，则x0=2x﹣8，y0=2y，
P（2x﹣8，2y）代入圆C中得（2x﹣7﹣3）2+（2y﹣2）2=13
即线段PQ中点M的轨迹方程为（x﹣5）2+（y﹣1）2= 
【解析】（1）设所求圆的方程为（x﹣a）2+（y﹣b）2=r2 ， 代入坐标，可得圆心与半径，即可求圆C的方程；（2）利用代入法，求线段PQ中点M的轨迹方程．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
【题目】对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计，做出甲的得分频率分布直方图如图所示，列出乙的得分统计表如表所示：
分值 | [0，10） | [10，20） | [20，30） | [30，40） |
场数 | 10 | 20 | 40 | 30 |
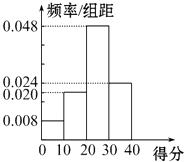
（1）估计甲在一场比赛中得分大于等于20分的概率．
（2）判断甲、乙两名运动员哪个成绩更稳定．（结论不要求证明）
（3）试利用甲的频率分布直方图估计甲每场比赛的平均得分．
