题目内容
如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值.
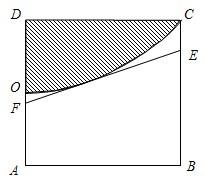

以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)
∵点C的坐标为(2,1),
∴22a=1,a=
故边缘线OC的方程为y=
x2(0≤x≤2).
要使梯形ABEF的面积最大,则EF所在的直线必与抛物线弧OC相切,设切点坐标为P(t,
t2)(0<t<2),
∵y′=
x,
∴直线EF的方程可表示为y-
t2=
t(x-t),即y=
tx-
t2,
由此可求得E(2,t-
t2),F(0,-
t2).
∴|AF|=|-
t2-(-1)|=1-
t2,|BE|=|(t-
t2)-(-1)|=-
t2+t+1,
设梯形ABEF的面积为S(t),则S(t)=
|AB|•[|AF|+|BE|]=(1-
t2)+(-
t2+t+1)=-
t2+t+2=-
(t-1)2+
≤
.
∴当t=1时,S(t)=
.,
故S(t)的最大值为2.5.此时|AF|=0.75,|BE|=1.75.
答:当AF=0.75m,BE=1.75m时,可使剩余的直角梯形的面积最大,其最大值为2.5m2.

∵点C的坐标为(2,1),
∴22a=1,a=
| 1 |
| 4 |
故边缘线OC的方程为y=
| 1 |
| 4 |
要使梯形ABEF的面积最大,则EF所在的直线必与抛物线弧OC相切,设切点坐标为P(t,
| 1 |
| 4 |
∵y′=
| 1 |
| 2 |
∴直线EF的方程可表示为y-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由此可求得E(2,t-
| 1 |
| 4 |
| 1 |
| 4 |
∴|AF|=|-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
设梯形ABEF的面积为S(t),则S(t)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴当t=1时,S(t)=
| 5 |
| 2 |
故S(t)的最大值为2.5.此时|AF|=0.75,|BE|=1.75.
答:当AF=0.75m,BE=1.75m时,可使剩余的直角梯形的面积最大,其最大值为2.5m2.


练习册系列答案
相关题目
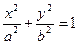 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=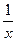 ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。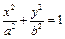 (a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且
(a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且 最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.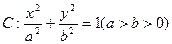 的离心率为
的离心率为 ,且曲线过点
,且曲线过点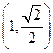
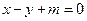 与椭圆C交于不同的两点A,B,且线段AB的中点不在圆
与椭圆C交于不同的两点A,B,且线段AB的中点不在圆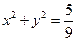 内,求
内,求 的取值范围.
的取值范围.