题目内容
【题目】已知动圆![]() 过定点
过定点![]() ,并且内切于定圆
,并且内切于定圆![]() ..
..
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,(1)中曲线上有两个点
,(1)中曲线上有两个点![]() ,并且
,并且![]() 三点共线,
三点共线,![]() 三点共线,
三点共线,![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 设动圆的半径为![]() ,则
,则![]() ,
,![]() 所以
所以![]() ,可得到轨迹为椭圆;(2)直线
,可得到轨迹为椭圆;(2)直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]() ,联立直线和椭圆方程得到二次方程,根据弦长公式得到
,联立直线和椭圆方程得到二次方程,根据弦长公式得到![]() ,
,![]() ,
,![]() ,通过换元得到
,通过换元得到![]() ,根据二次函数的性质得到最值即可.
,根据二次函数的性质得到最值即可.
(1)设动圆的半径为![]() ,则
,则![]() ,
,![]() 所以
所以![]() 由椭圆的定义知动圆圆心
由椭圆的定义知动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,
为焦点的椭圆,![]() 所以
所以![]() ,动圆圆心
,动圆圆心![]() 的轨迹方程是
的轨迹方程是![]() ;
;
(2)当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() 的斜率为0,易得
的斜率为0,易得![]() ,四边形
,四边形![]() 的面积
的面积![]()
当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]() 联立方程得
联立方程得
![]() ,消元得
,消元得![]()
设![]() 则
则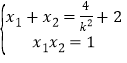
![]()
![]()
![]() 直线
直线![]() 的方程为
的方程为![]()
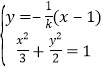 ,得
,得![]()
设![]() 则
则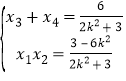
![]()
四边形![]() 的面积
的面积![]()
令![]() ,
,![]() ,上式
,上式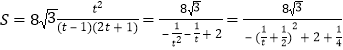
![]() ,由二次函数图像可知
,由二次函数图像可知![]() 的范围是
的范围是![]()
![]()
综上可得![]() ,最小值为
,最小值为![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

