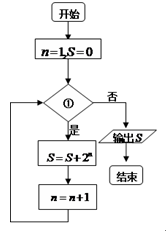
题目内容
甲,乙两个同学同时报名参加某重点高校2013年自主招生考试,高考前自主招生的程序为审核材料文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格,已知甲、乙两人审核过关的概率分别为
,
,审核过关后,甲,乙两人文化课测试合格的概率分别为
,
.
(1)求甲,乙两人至少有一个通过审核的概率;
(2)设X表示甲,乙两人中获得自主招生入选资格的人数,求X的分布列和数学期望.
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 4 |
| 4 |
| 5 |
(1)求甲,乙两人至少有一个通过审核的概率;
(2)设X表示甲,乙两人中获得自主招生入选资格的人数,求X的分布列和数学期望.
(1)设A为”甲,乙两人至少有一人通过审核”,则P(A)=1-(1-
)(1-
)=
故甲,乙两人至少有一个通过审核的概率为
;
(2)X的可能取值为0,1,2P(X=0)=(1-
×
)(1-
×
)=
,P(X=2)=(
×
)(
×
)=
,P(X=1)=1-P(X=0)-P(X=2)=
.
∴X的分布列为
EX=0×
+1×
+2×
=
,
故X的数学期望为
.
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
故甲,乙两人至少有一个通过审核的概率为
| 4 |
| 5 |
(2)X的可能取值为0,1,2P(X=0)=(1-
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
| 4 |
| 5 |
| 33 |
| 100 |
| 3 |
| 5 |
| 3 |
| 4 |
| 1 |
| 2 |
| 4 |
| 5 |
| 18 |
| 100 |
| 49 |
| 100 |
∴X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 33 |
| 100 |
| 49 |
| 100 |
| 18 |
| 100 |
| 17 |
| 20 |
故X的数学期望为
| 17 |
| 20 |

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 服从以下分布:
服从以下分布:
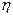 服从二项分布
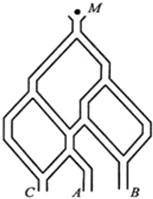
服从二项分布 .
.

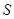 是
是 ,则①应为( )
,则①应为( )