题目内容
【题目】一个圆锥的底面半径为2，高为6，在其中有一个高为x的内接圆柱．
(1)用x表示圆柱的轴截面面积S；
(2)当x为何值时，S最大？
【答案】(1) S＝－
x2＋4x(0<x<6)．
(2) 当x＝3时，S最大，最大值为6.
【解析】分析：（1）画出圆锥的轴截面，将空间问题转化为平面问题，然后根据相似三角形的性质和比例的性质，得出内接圆柱底面半径r与x关系式即可
（2）根据二次函数的性质易得到其最大值，及对应的x的值．
详解：
画出圆柱和圆锥的轴截面，
如图所示，
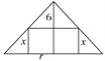
设圆柱的底面半径为r，则由三角形相似可得
＝
，解得r＝2－
.
(1)圆柱的轴截面面积
S＝2r·x＝2·(2－)·x＝－x2＋4x(0<x<6)．
(2)∵S＝－x2＋4x＝－(x2－6x)
＝－(x－3)2＋6，
∴当x＝3时，S最大，最大值为6.
练习册系列答案
相关题目
